Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 5.Problemas - Ex. 30
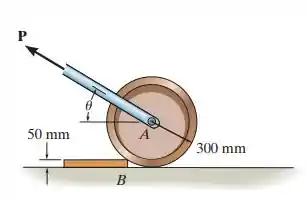
Determine a intensidade e a direção da força mínima necessária para puxar o rolete de sobre o degrau liso
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Antes de explicarmos a questão, vamos começar fazendo o diagrama de forças do nosso problema. Lembrem-se que o contato com superfícies lisas gera forças normais!
Então, teremos o seguinte diagrama:
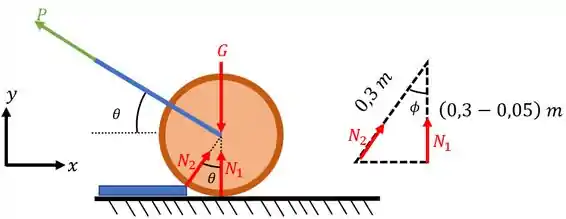
OBS: destaque para o triângulo ao lado do diagrama de forças para nos auxiliar na identificação do ângulo .
A questão pede para determinarmos a força mínima e a direção necessária para que o rolete descole do plano da base!
Em outras palavras, precisamos determinar a força mínima para que a força normal é nula!
Agora que já entendemos o que fazer, basta lembrarmos das equações de equilíbrio, as quais são:
Então, vamos as contas!
Passo 2
Utilizando as equações do equilíbrio, vamos fazer o somatório de forças, tanto na direção quanto na direção . Desta forma, obtemos:
Como ainda não determinarmos o ângulo , não conseguimos seguir com os cálculos. Este ângulo será dado por:
Fazendo e sabendo que , temos:
E assim chegamos a seguinte função:
Isto é, a força como uma função da direção . Minimizando esta função, obtemos: e .