Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas - Ex. 62

Determine a intensidade e a direção da força resultante que atua sobre o encanamento.

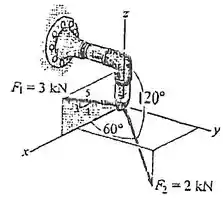
Passo 1

Vamos decompor as foças como vetor cartesiano:

Nossa F 1 está no plano x z , então terá duas componentes e vamos encontrar pela relação dos catetos e hipotenusa do triângulo dado:

F 1 x = F 1   4 5 = 3   k   4 5

F 1 x = 2,4   k N

F 1 z = F 1   3 5 = 3   k   3 5

F 1 z = 1,5   k N

Assim, nosso vetor cartesiano fica:

F 1 = 2,4 i + 1,5 k   k N

Passo 2

Agora para F 2 usaremos os ângulos diretores, como tempos apenas dois vamos encontrar o terceiro pela relação:

cos 2 ⁡ α + cos 2 ⁡ β + cos 2 ⁡ γ = 1

Logo:

cos 2 ⁡ 60 ° + cos 2 ⁡ β + cos 2 ⁡ 120 ° = 1

β = cos - 1 ⁡ 1 - cos 2 ⁡ 120 ° - cos 2 ⁡ 60 °

β = 45 °

Passo 3

E assim encontrar nossas componentes de F 2 :

F x = F cos ⁡ α

F x = 2  k  cos ⁡ 60 °

F x = 1,0   k N

F y = F cos ⁡ β

F y = 2   k cos ⁡ 45 °

F y = 1,4   k N

F z = F cos ⁡ γ  

F z ⁡ = 2   k cos ⁡ 120 °  

F z = ⁡ - 1   k N  

Logo, nosso vetor cartesiano para F 2 fica:

F 2 = 1 i + 1,4 j - 1 k   k N

Passo 4

Para encontrar a força resultante somamos nossas forças agindo no encanamento:

F R = 2,4 i + 1,5 k k + 1 i + 1,4 j - 1 k k

F R = 3,4 i + 1,4 j + 0,5 k   k N

Sua intensidade em módulo será:

| F R |   = F R x 2 + F R y 2 + F R z 2

| F R |   = 3,4 2 + 1,4 2 + 0,5 2

| F R | = 3,7   N

Passo 5

Por último encontramos a direção da força através dos seus ângulos coordenados diretores:

cos ⁡ α = F x F ∴ α = cos - 1 ⁡ F x F  

cos ⁡ β = F y F   ∴ β = cos - 1 ⁡ F y F

cos ⁡ γ = F z F   ∴ γ = cos - 1 ⁡ F z F

Então:

α = cos - 1 ⁡ 3,4 3,7 = 23 °

β = cos - 1 ⁡ 1,4 3,7 = 68 °

γ = cos - 1 ⁡ 0,5 3,7 = 8 2 °

Resposta

| F R | = 3,7   N

α = 23 °

β = 68 °

γ = 82 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas forças atuam sobre o gancho. Determine o ângulo θ entre elas. Além disso, quais são as projeções de F 1 e F 2 ao longo do eixo y?
Determine a projeção da força F = 80 N ao longo da linha B C . Expresse o resultado como um vetor cartesiano.
Determine a intensidade da componente projetada da força F a c que atua ao longo eixo z .
Determine a projeção da força F = 400 N que atua ao longo da linha A C do encanamento. Expresse o resultado como um vetor cartesiano.
Determine o comprimento do lado B C da chapa triangular. Resolva o problema calculando a intensidade de r b C . Depois verifique o resultado calculando primeiro θ ,r a b , r A c e em seguida usando a