Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 4.Problemas Fundamentais - Ex. 28
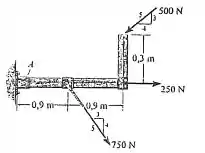
Substitua o carregamento do sistema por uma força e momento de binário resultante equivalente agindo no ponto .
Passo 1
Falaaa!
A questão pede para substituirmos todas as forças do problema por uma força resultante e um momento de binário resultante com relação ao ponto . Para isso, o primeiro passo é decompor as forças e escrevê-las como vetores.
A componente horizontal de , achamos multiplicando essa força por , usando a proporção do triângulo 3/4/5 que ele deu como orientação. Na componente vertical a gente usa . E como ambas estão no sentido negativo de seus eixos
está somente no eixo , no sentido positivo:
E para a componente horizontal a gente acha multiplicando por , e a vertical por . Reparando que a componente vertical está para baixo, aí ela fica negativa:
Para acharmos a resultante de forças em , o que a gente pode fazer é somar as forças que a gente tem, achando a resultante.
Aí como lindamente escrevemos as forças com carinha de vetor, o que a gente precisa fazer é o somar cada componente separadamente.
Desta forma, a força resultante será:
Onde , e .
Passo 2
Para o binário, basta calcular o momento de cada força com relação ao ponto e somar cada um. Vamos usar a forma vetorial para facilitar essa soma. Lembrando a definição de momento:
Onde é a força que causa o momento. E é o vetor que sai do ponto onde a gente quer calcular o momento e vai até o ponto de aplicação da força.
Considerando como origem. Para , o ponto de aplicação dela é
Aí o vetor que sai de e vai para esse ponto
E para :
E por fim para
Passo 3
Assim,
Somando todos os momentos:
Onde , e .