Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas - Ex. 61
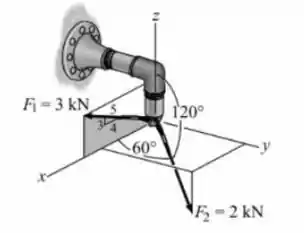
Expresse cada força que atua sobre o encanamento na forma de vetor cartesiano.
Passo 1
Fala ai galerinha bonita, tudo beleza? Nesse exercício aqui a gente tem duas forças e atuando sobre um encanamento mais ou menos como nessa figura aqui:
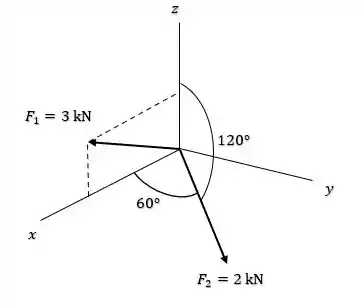
Sabendo disso, o enunciado nos pede pra escrever as forças na forma de vetores cartesianos, ou seja, precisamos colocar os vetores em termos de suas componentes de cada eixo e , dada como:
Passo 2
Iradoso, vamos começar pela força , ela possui componentes somente no plano , tal que:
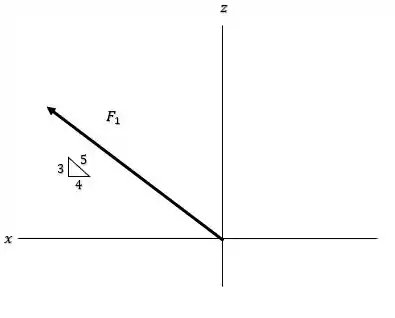
Aquele triângulo, conhecido como triângulo “345”, diz pra gente qual o ângulo que força está fazendo com eixo :
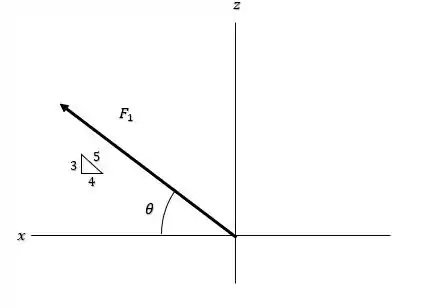
Ou seja, é o mesmo ângulo que o triângulo “345” possui, de modo que as relações trigonométricas de seno e cosseno serão as mesmas, logo:
Então isso quer dizer que as componentes da força serão dadas como:
E para o eixo :
E como não possui componentes em , , teremos que sua forma vetorial será dada como:
Passo 3
Agora para podemos usar as relações de ângulos que existem entre o vetor e os eixos e , de modo que:
E para o eixo :
Agora para descobrir o valor de podemos lembrar que:
Logo:
Substituindo os valores que conhecemos vamos descobrir que:
Portanto, o vetor cartesiano será expresso como:
