Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 34a

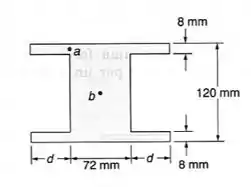
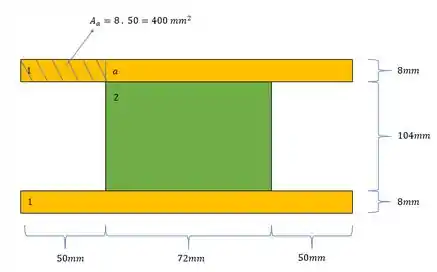
Para a viga de seção transversal mostrada, submetida a uma força cortante vertical de 25   k N , determinar a tensão de cisalhamento, quando d = 50 m m , no:

  1. Ponto a

Passo 1

Nosso objetivo é determinar a tensão cisalhante no ponto “a”, devido a um cortante, com isso sabemos que a equação é dada por:

τ = V Q I b

Em que:

V = c o r t a n t e   a g i n d o   n a   s e ç ã o  

Q = m o m e n t o   e s t á t i c o  

I = m o m e n t o   d e   i n é r c i a  

b = e s p e s s u r a   d a   r e g i ã o   q u e   d e s e j a   s e   s a b e r   a   t e n s ã o  

Para esses dados sabemos que:

V = 25   k N = 25000   N

t a = 8 m m

Agora precisamos determinar o momento estático e o momento de inércia, para isso temos um passo a passo.

Passo 2

Vamos determinar primeiro o momento de inércia, para isso precisamos determinar algumas coisas, para isso temos que fazer o seguinte passo a passo.

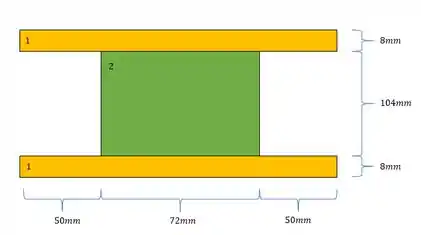
  • Primeiro determinamos uma divisão em seções mais simples

  • Em segundo determinamos as áreas da nossa seção

  • Em terceiro determinamos a distância dos centroides dos elementos até a LN, e como a seção é simétrica, está no centro da seção total, sendo assim teremos que:

  • Em quarto precisamos determinar os momentos de inércia de cada uma das seções mais simples:

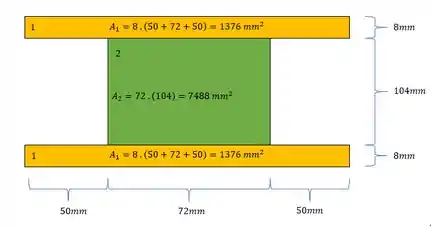
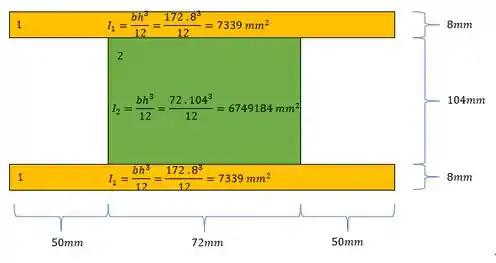
    • Agora para determinarmos o momento de inércia, precisamos fazer a seguinte conta:

    I = ∑ I i + A i d i 2

    Mas temos que lembrar que precisamos usar os valores de inercia da região 6 como negativa, sendo assim temos que:

    I = 2 ( I 1 + A 1 d 1 2 ) + I 2 + A 2 d 2 2

    I = 2 ( 7339 + 1376   .     56 2 ) + 6749184 + 7488   .     0 2

    I = 15394134   m m 4

    Passo 3

    Para o momento estático precisamos determinar os seguintes dados:

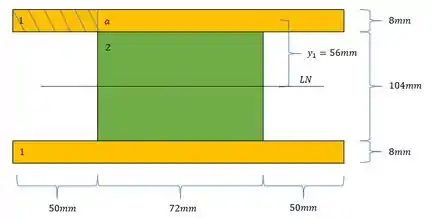
  • Área da região acima do ponto que se quer saber o cisalhamento

  • Distância do centroide da área até a LN

agora para determinar o momento estático precisamos fazer a seguinte conta:

Q = A a y a = 400   .   5 6 = 22400   m m 3

Substituindo na equação, teremos que:

τ = V Q I b = 25000   .   22400     15394134     .     8 = 4,55 N m m 2 = 4,55   M P a

Resposta

τ = 4,55   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a viga e o carregamento do Prob 5.92 , determinar: ( a ) o valor de β para que a tensão normal no ponto b seja zero; ( b ) a correspondente tensão normal no ponto a .
Sabendo-se que o tubo estrutural mostrado tem uma espessura da parede uniforme de 8m m , determinar a tensão de cisalhamento em cada um dos dois pontos indicados.
Para a viga extrudada, com a seção transversal mostrada, determinar a localização do centro de cisalhamento O.
Determinar a localização do centro de cisalhamento O, de uma viga de parede fina de espessura uniforme e com a seção transversal mostrada.
Resolver o Prob 5.95 , considerando que a força de 65k N aplicada no ponto A atua verticalmente para baixo.