Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 9.Problemas - Ex. 6
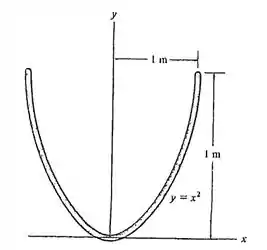
Determine a localização do centroide do fio.
Passo 1
Fala! A gente quer o centroide desse arco. Como temos um arco, a gente precisa separar um pedacinho dele, chamado de elemento diferencial. Isso vai nos ajudar a montar a integral para achar o comprimento do arco e para usar as fórmulinhas do centroide.
Vamos começar enxergando nosso elemento diferencial, ele é o comprimento de um pedacinho do nosso arco, como mostrado na figura:
Como a espessura desse arco é desprezível, consideramos que ele só tem comprimento. Mas a gente precisa escrever esse comprimento dele em função de e . Observe que:
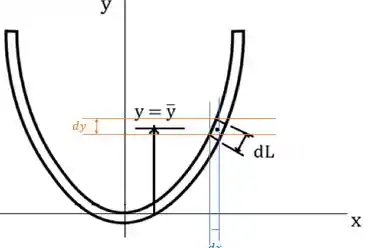
Aí usando o bom e velho Pitágoras chegamos em:
Vamos aproveitar e extrair o da raiz:
Olha lá, ficou um ainda dentro, isso tem cara de derivada. Sabendo que , derivando temos então:
Logo, nosso fica:
Passo 2
Para obter o nosso comprimento somaremos todos os pedacinhos elementares da curva através da integral. Já que temos uma parábola os limites se integração serão e (intervalo onde nossa parábola está em relação a ) como mostra a figura.
Resolvendo essa integral por substituição trigonométrica aproveitando a tabelinha:
Nosso será , logo
E os limites de integração:
Aí nossa integral fica:
Lembrando que temos uma identidade trigonométrica que diz :
E para resolver essa integral envolvendo o , precisamos usar uma fórmulinha de redução de integrais trigonométricas em que teremos:
Passo 3
Passamos então para o centroide da nossa barra. Vemos que nosso por simetria se encontra em .
Para temos que:
Sabendo que nosso e usando do passo 1, logo, nosso fica:
Resolvendo essa integral também por substituição trigonométrica, chegamos em:
E então:
Você também pode usar tabelinhas de integrais. Só vê o que seu prof prefere nesses casos onde a integral é mais feinha.
Logo, nosso centroide fica: