Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 3.Problemas - Ex. 60
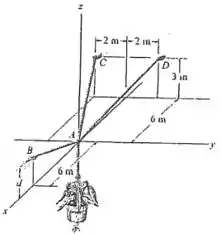
O vaso de é sustentado por A, pelos três cabos. Determine a força que atua em cada cabo para o equilíbrio. Considere .
Passo 1
Olá, belezinha? Bora fazer esse exercício top? Bora!!
Para encontrarmos o valor da tração em cada cabo, o que deve ser feito primeiramente é o diagrama de corpo livre no qual serão representadas as forças envolvidas. Assim, teremos:
Em seguida, o equilíbrio de forças deve ser analisado nas três dimensões , pelo fato de as forças estarem atuando em todos esses três sentidos.
Tem-se que o vaso exerce uma força peso para baixo que tem intensidade de .
O que vamos fazer aqui é usar as equações de equilíbrio que dizem que
No ponto. Como a gente está em 3D, é melhor colocar as forças na forma vetorial primeiro e depois achar as componentes delas em cada eixo. Aí as equações de equilíbrio que a gente vai usar são:
Bora lá!
Passo 2
Para achar a forma vetorial das forças, vamos usar a fórmulinha:
Como o módulo das forças a gente vai achar pelas equações de equilíbrio, só precisamos achar o vetor que está na direção e sentido da força do por enquanto.
A força sai de e vai para . Aí para achar o vetor nessa direção, a gente faz ponto final menos inicial
Então:
Para achar as componentes da força é só olhar as componentes do vetor que a gente achou
Para , nosso vetor sai de e vai para :
Assim:
Onde:
Para , nosso vetor sai de e vai para :
Assim:
Onde:
Passo 3
Conseguimos montar as equações de equilíbrio.
A condição de equilíbrio requer quer que o somatório de forças em cada eixo seja nulo (para que nenhum corpo se mova), ou seja:
Aí a gente vai usar para cada eixo as componentes que achou e peso. Lembrando que o peso só atua no eixo e para baixo, por isso ele entra negativo no somatório.
Adotando o sentido dos eixos mostrado no desenho do enunciado:
Passo 4
Agora, como há três equações encontradas, é possível montar um sistema de equações e determinar a solução dele, cuja solução será o valor das forças.
Vamos utilizar o sistema de matrizes para resolver esse sistema, logo:
Resolvendo por cramer, teremos:
O determinante é
O determinante com a substituição em x, é de
O determinante com a substituição em y, é de
O determinante com a substituição em z, é de
Logo;
Resolvendo este sistema, pode se obter: