Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.3 - Ex. 25
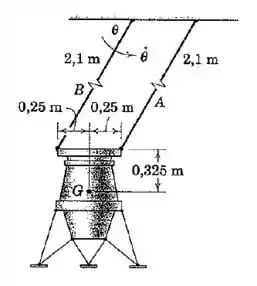
Os testes de projeto da sequência de aterrissagem para o módulo lunar são realizados utilizando o modelo de pêndulo suspenso pelos fios paralelos e . Se o modelo possui uma massa de , com centro de massa em , e se quando , calcule a tração em cada um dos fios para esse instante:
Passo 1
Nós temos duas variáveis: e , que são as trações nos fios. Isso quer dizer que vamos precisar de duas equações para resolver o problema.
Vamos montar uma equação de momentos e uma equação de forças.
Como o sistema se move como um pêndulo, ele não tem rotação em torno do ponto , podemos escrever que:
Essa será nossa equação de momentos. E a equação de forças?
Como o sistema descreve um movimento circular com velocidade angular , nós sabemos que a soma das forças que apontam para o centro da trajetória circular são:
Beleza, essa é uma boa forma de resolver o problema.
Passo 2
Vamos começar calculando a soma dos momentos em relação ao ponto :
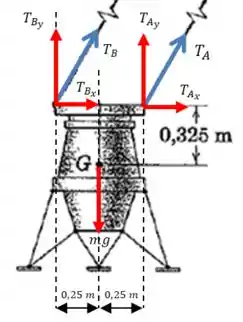
Então apenas as trações geram momento em relação ao ponto :
Como e formam um ângulo de com a horizontal:
Beleza, essa é nossa primeira equação.
Passo 3
Agora vamos montar a equação das forças:
Qual é a direção que aponta para o centro da trajetória? É justamente a direção das duas forças de tração:
Onde é a componente da força peso na direção de :
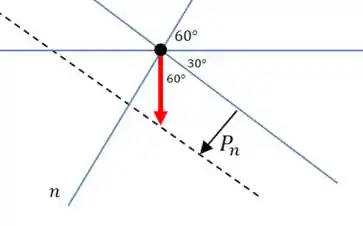
Então nossa segunda equação é:
Passo 4
Agora ficamos com o seguinte sistema:
Substituindo a primeira equação na segunda:
E agora substituindo isso na segunda equação:
Resposta
As trações são e .