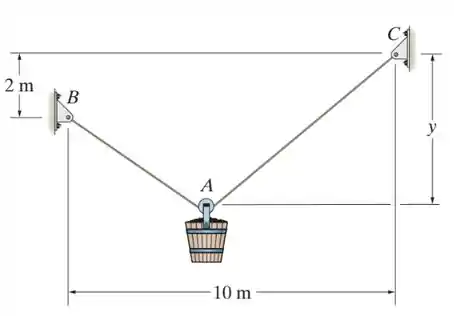
O balde e seu conteúdo têm uma massa de . Se a corda BAC possui comprimento, determine a distância y até a polia em A para o equilíbrio. Despreze a dimensão da polia.

Fala aí galera tudo bem??? Espero que simmm!!! Bora lá e vamos começar desenhando o diagrama de corpo livre.

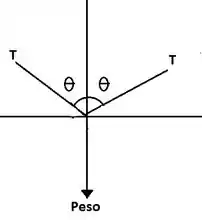
Vale lembrar que como a polia é ideal as tensões são iguais. Então temos que fazer o somatório das forças que devem ser iguais a zero.

Analisando as forças sabe-se que T é a tração no cabo preso aos pontos B e C e P é a força peso. Para que haja o equilíbrio das forças, a somatória delas deve ser zero. Analisando o eixo x:



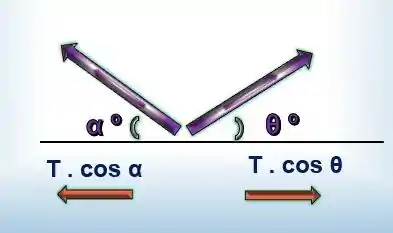
Simplificando T, temos:

Logo:

O desenho agora pode ser entendido como 2 triângulos conforme visto abaixo:

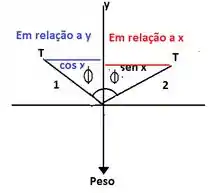
Gurizada nomeei os 2 triângulos como “1” e “2” para facilitar o entendimento dos cálculos. Vamos chamar de x a medida da hipotenusa de (2), logo a hipotenusa de (1) vale 10−x, pois o fio tem 10m de comprimento.

A medida da base (b) do triângulo (2) vale, por Pitágoras:

Galera se o comprimento das 2 bases valem 15 vamos considerar o seguinte:

Por semelhança de triângulos temos o seguinte:

Repare que, essencialmente, a equação não mudou nada

Agora que temos as relações dos triângulos semelhantes podemos manipular ainda mais

Agora vamos dividir tudo por

Mas isso é igual a

Vamos manipular só um pouquinho mais, a gente tem que sumir com a raiz e depois isolar o x

Então