Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 5.Problemas - Ex. 54
5.54. A barra uniforme AB possui peso de e a mola está descarregada quando . Se , determine a rigidez da mola.
Passo 1
Beleza, se podemos dividir essa figura em dois triângulos
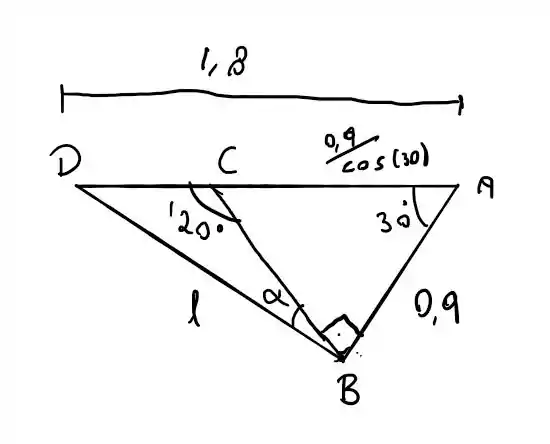Sabemos que a soma dos ângulos internos de um triângulo é 180°, por isso podemos determinar aquele ângulo como 60°.
Usando trigonometria podemos determinar
Sabemos que BC é
Sabemos também que DA é e que
Então
E aí finalmente podemos determinar usando a lei dos cossenos
Passo 2
Agora podemos usar a lei dos senos para determinar o ângulo
Então
Passo 3
Finalmente podemos usar as equações de equilíbrio para obter a força da mola
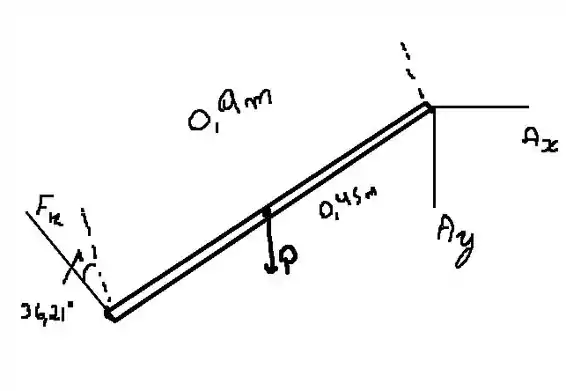
Vamos isolar
Fazendo todas as contas
Passo 4
Mas não queremos , queremos k
Vamos fazer então
é o tamanho da mola menos o tamanho da mola quando está relaxada. Sabemos que o tamanho da mola é e quando ela está relaxada, que é quando temos
Então
Agora temos tudo para determinar