Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 3.Problemas - Ex. 22

3.22. Uma força vertical P = 50   N é aplicada nas extremidades da corda AB de 0,6   m e na mola AC. Se a mola tem um comprimento não deformado de 0,6   m , determine o ângulo θ

Para o equilíbrio. Considere k = 250 N m

Passo 1

Vamos começar calculando a força da mola F k

lembrando

F k = k ⋅ x

O k nos é dado no exercício, então vamos calcular x .

x é a medida da mola em relação a sua medida quando relaxada.

A medida da mola na imagem pode ser calculada pela lei dos cossenos, veja o triângulo

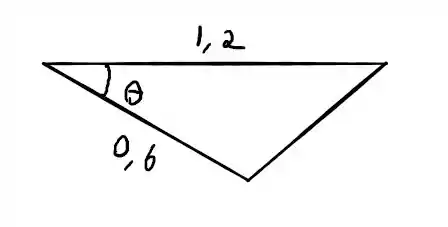
Então

x = 1,2 2 + 0,6 2 - 2 ⋅ 1,2 ⋅ 0,6 ⋅ cos ⁡ θ - 0,6

Fazendo todos os cálculos

x = 1,8 - 1,44 ⋅ cos ⁡ θ - 0,6

O que nos dá

F k = k ⋅ x = 250 ⋅ 1,8 - 1,44 ⋅ cos ⁡ θ - 0,6

Passo 2

Agora vamos usar as equações de equilíbrio. Para o ponto A temos

F R x = 0

F R x = F k ⋅ cos ⁡ ϕ - T ⋅ cos ⁡ θ = 0

F k ⋅ cos ⁡ ϕ = T ⋅ cos ⁡ θ     ( 1 )

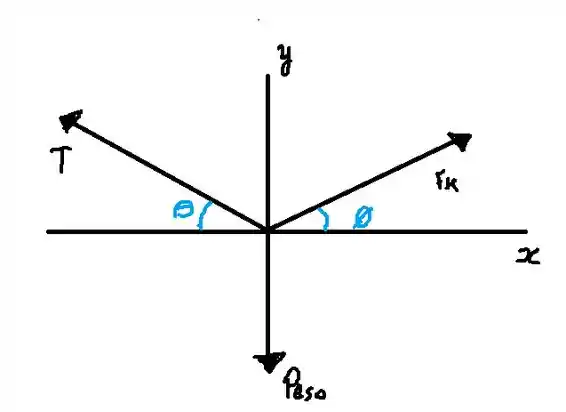
E para o eixo y

F R y = 0

F R y = F k ⋅ sin ⁡ ϕ + T ⋅ sin ⁡ θ - 50 = 0

F k ⋅ sin ⁡ ϕ = 50 - T ⋅ sin ⁡ θ     ( 2 )

Dessas equações podemos determinar T em termos de θ

De (1) temos

T = F k ⋅ cos ⁡ ϕ cos ⁡ θ

Passo 3

Para determinar cos ⁡ ϕ e sin ⁡ ϕ podemos usar esse triângulo

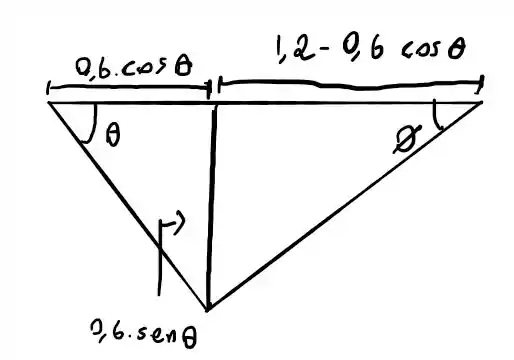
Então temos o triângulo onde

c a t e t o   o p o s t o = 0,6 ⋅ sin ⁡ θ c a t e t o   a d j a c e n t e = 1,2 - 0,6 ⋅ cos ⁡ θ h i p o t e n u s a = 1,8 - 1,44 ⋅ cos ⁡ θ

Então

cos ⁡ ϕ = 1,2 - 0,6 ⋅ cos ⁡ θ 1,8 - 1,44 ⋅ cos ⁡ θ  

E

sin ⁡ ϕ = 0,6 ⋅ sin ⁡ θ 1,8 - 1,44 ⋅ cos ⁡ θ

Então (1) fica

T = F k ⋅ 1,2 - 0,6 ⋅ cos ⁡ θ 1,8 - 1,44 ⋅ cos ⁡ θ   ⋅ 1 cos ⁡ θ

Passo 4

Agora vamos substituir os valores na equação (2)

F k ⋅ sin ⁡ ϕ = 50 - T ⋅ sin ⁡ θ    

F k ⋅ 0,6 ⋅ sin ⁡ θ 1,8 - 1,44 ⋅ cos ⁡ θ = 50 - F k ⋅ 1,2 - 0,6 ⋅ cos ⁡ θ 1,8 - 1,44 ⋅ cos ⁡ θ   ⋅ 1 cos ⁡ θ ⋅ sin ⁡ θ  

F k ⋅ 0,6 ⋅ sin ⁡ θ 1,8 - 1,44 ⋅ cos ⁡ θ + F k ⋅ 1,2 - 0,6 ⋅ cos ⁡ θ 1,8 - 1,44 ⋅ cos ⁡ θ   ⋅ tan ⁡ θ = 50  

Mas também sabemos o valor de F k

250 1,8 - 1,44 cos ⁡ θ - 0,6 0,6 sin ⁡ θ 1,8 - 1,44 cos ⁡ θ + 250 1,8 - 1,44 cos ⁡ θ - 0,6 1,2 - 0,6 cos ⁡ θ 1,8 - 1,44 cos ⁡ θ   tan ⁡ θ = 50  

Equação grandinha né?

Mas o ponto é que essa equação só depende de θ , então estamos perto do resultado

Vamos dar uma simplificada

Podemos dividir os dois lados por 250

1,8 - 1,44 cos ⁡ θ - 0,6 0,6 sin ⁡ θ 1,8 - 1,44 cos ⁡ θ + 1,2 - 0,6 cos ⁡ θ 1,8 - 1,44 cos ⁡ θ   tan ⁡ θ = 1 5  

  1,8 - 1,44 cos ⁡ θ - 0,6 0,6 sin ⁡ θ + 1,2 tan ⁡ θ - 0,6 cos ⁡ θ tan ⁡ θ 1,8 - 1,44 cos ⁡ θ = 1 5  

0,6 sin ⁡ θ + 1,2 tan ⁡ θ - 0,6 cos ⁡ θ tan ⁡ θ - 0,6 0,6 sin ⁡ θ + 1,2 tan ⁡ θ - 0,6 cos ⁡ θ tan ⁡ θ 1,8 - 1,44 cos ⁡ θ = 1 5

Vamos fazer uma jogadinha matemática no termo

0,6 cos ⁡ θ t a n θ = 0,6 cos ⁡ θ ⋅ sin ⁡ θ cos ⁡ θ = 0,6 sin ⁡ θ  

Então

0,6 sin ⁡ θ + 1,2 tan ⁡ θ - 0,6 sin ⁡ θ - 0,6 0,6 sin ⁡ θ + 1,2 tan ⁡ θ - 0,6 sin ⁡ θ 1,8 - 1,44 cos ⁡ θ = 1 5

1,2 tan ⁡ θ - 0,6 1,2 tan ⁡ θ 1,8 - 1,44 cos ⁡ θ = 1 5

Agora colocamos o 1,2 tan ⁡ θ em evidência

1,2 tan ⁡ θ 1 - 0,6 1 1,8 - 1,44 cos ⁡ θ = 1 5

1,2 passa dividindo

tan ⁡ θ 1 - 0,6 1 1,8 - 1,44 cos ⁡ θ = 1 6

Ufa!!!

Chegamos finalmente.

Daqui podemos tirar que

θ ≈ 35 °

Resposta

θ = 35 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Exercício de Livro
Os membros AC e AB suportam a caixa de 100 kg. Determine a força de tração desenvolvida em cada membro.
Exercício de Livro
O comprimento não deformado da mola A B é 3m . Se o bloco é mantido na posição de equilíbrio mostrada, determine a massa do bloco em D .
Exercício de Livro