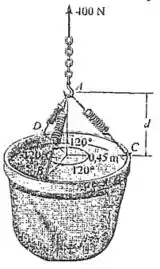
O balde possui um peso de e está suspenso por três molas, cada uma com comprimento não deformado de e rigidez de . Determine a distância vertical da borda do balde ao ponto A para o equilíbrio.
Passo 1
Fala aaai galerinha bonita, tudo beleza? Bora lá fazer essa questão, pra gente encontrar o valor de , o que deve ser feito primeiramente é o diagrama de corpo livre no qual serão representadas as forças envolvidas:
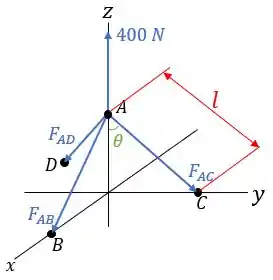
Onde é o comprimento da mola e é o ângulo formado entre cada cabo e o eixo .
Como a borda do balde possui uma simetria (divide-se em partes com o mesmo comprimento e mesmo ângulo) e as distâncias do seu centro até os pontos são iguais, então a tração será a mesma em cada cabo.
Assim, lembrando que a força de uma mola é dada pela Lei de Hooke:
Onde é a variação da mola, temos que , tal que:
Passo 2
Com o diagrama de corpo livre, podemos fazer o desenho de um triângulo no eixo :
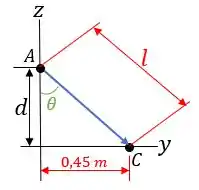
Para vermos que:
E, então, conseguimos montar as equações de equilíbrio.
Passo 3
O equilíbrio requer quer que o somatório de forças em cada dimensão seja nulo. Porém, a única força dada pelo enunciado está no eixo .
Logo, adotando o sentido dos eixos mostrado no diagrama de corpo livre:
Em que as forças em são da corrente e das molas :
Mas como as forças das molas são iguais:
Podemos reescrever como:
Lembrando que a força da mola é:
Como o enunciado nos deu que , teremos que:
Substituindo o valor da rigidez :
Tirando o fator comum e encontrando o MMC dos parênteses:
Vamos isolar as constantes de um lado só da equação:
Como:
Podemos escrever a equação como:
Ou ainda:
Passo 4
Mas agora que vem a malandragem, porque podemos escrever as funções seno e tangente em função da distância , tal que:
Então se a gente substituir isso na nossa relação, teremos que:
Então se a gente elevar ao quadrado dos dois lados, vamos ter que:
E se a gente colocar esse polinômio numa calculadora, vamos obter que:
Portanto: