Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Hibbeler - Estática- Ed: 14º - Capítulo 10.Problemas - Ex. 66

66. Determine o produto de inércia da área da seção transversal em relação aos eixos u e v .

Passo 1

Eaiii.... beleza???

Nessa questão vamos precisar lembrar o momento de inércia de formas retangulares:

I = 1 12 b h 3

E usar a equação para momento de inércia em eixos inclinados:

I u v = I x - I y 2 sen ⁡ 2 θ + I x y cos ⁡ 2 θ

Passo 2

Calculando o momento de inércia em relação ao eixo x:

Vamos calcular o momento de inércia do retângulo preenchido e depois tiramos os buracos.

I x = 1 12 300 400 3 - 2 1 12 140 360 3

I x = 511 × 10 6   m m 4

E em relação ao eixo y:

Vamos dividir em três partes e somamos.

I y = 1 12 360 20 3 + 2 1 12 20 300 3

I y = 90,2 × 10 6   m m 4

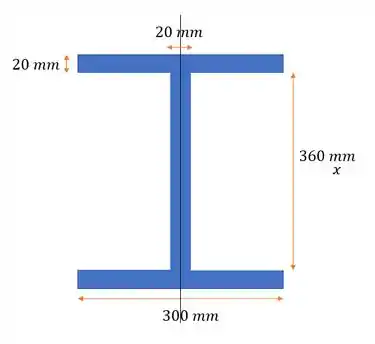
Quando a gente divide a viga em três partes, os centros de massa das três estão na mesma linha, então:

I x y = 0

Passo 3

Agora, então, aplicamos a equação:

I u v = I x - I y 2 sen ⁡ 2 θ + I x y cos ⁡ 2 θ

I u v = 511 × 10 6 - 90,2 × 10 6 2 sen ⁡ 2 20 + 0 cos ⁡ 2 20

I u v = 135 × 10 6   m m 4

E acabamos essa... bora pra próxima??

Resposta

I u v = 135 × 10 6   m m 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma barra delgada e uniforme de massa M e comprimentoL é encurvada no seu centro, de modo que os dois segmentos passam a ser perpendiculares um ao outro. Ache o momento de inércia em relação a um eixo
a) Para a placa retangular fina indicada na parte (d) da Tabela 9.2, ache o momento de inércia em relação a um eixo situado sobre o plano da placa passando pelo seu centro e paralelo ao eixo indicado
Use o teorema dos eixos paralelos para mostrar que os momentos de inércia das partes (a) e (b) da Tabela 9.2 são coerentes.
Em relação à qual eixo uma esfera uniforme de madeira leve possui o mesmo momento de inércia de uma casca esférica de chumbo de mesma massa e raio em relação a um diâmetro?
Uma haste metálica delgada, de comprimento d e massa M , pode girar livremente em torno de um eixo horizontal, que a atravessa perpendicularmente, à distância d / 4 de uma extremidade. A haste é solta