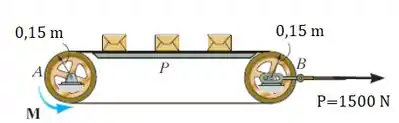
Determine o número máximo de pacotes de que podem ser colocados na esteira sem fazer com que a esteira deslize na roda de acionamento que está girando com uma velocidade angular constante. A roda está livre para girar. Além disso, determine o momento de torção correspondente que deve ser fornecido à roda . A esteira rolante está pré-tracionada com a força horizontal de . O coeficiente de atrito cinético entre a esteira e a plataforma é , e o coeficiente de atrito estático entre a esteira e a borda de cada roda é
Passo 1
Vamos desenhar o diagrama de corpo livre dessa situação para entendermos a situação da nossa questão!
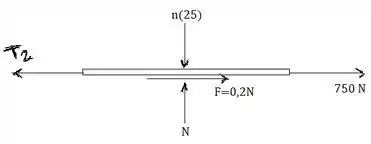
Passo 2
Para uma situação de equilíbrio, temos que o somatório das forças em e deve ser igual a zero. Portanto, assumindo como referencial positivo a direção para cima, temos:
Assumindo como referencial positivo a direção para direita, temos:
Passo 3
Vamos considerar que a roda está na iminência de escorregar, beleza? Seja , e Então, aplicando a equação para o atrito entre corda e roldana, temos:
Passo 4
O somatório dos momentos em relação a um determinado ponto, para um sistema em equilíbrio, deve ser igual a zero. Assim, para a nossa situação, temos o seguinte dagrama de corpo livre:
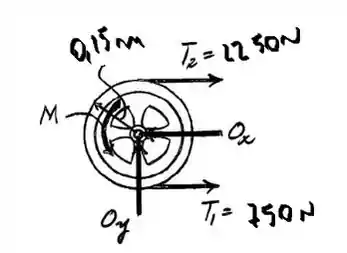
Adotando como sentido positivo o anti-horário, temos:
Resposta
O número máximo de pacotes é:
O momento de torção é igual a: