Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 4.Problemas - Ex. 108

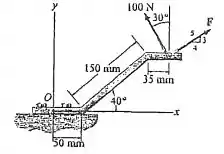
Substitua as duas forças por uma força e momento de binário equivalente no ponto . Considere .

Passo 1

Falaa!

O problema pede substituirmos o sistema de forças apresentado por uma força resultante e um momento de binário equivalente no ponto . O que a gente precisa fazer aqui na real é achar o somatório de forças e o somatório de momentos em relação a , e isso vai ser a nossa resposta.

Para isso, precisamos escrever as forças que agem sobre o sistema. Para fazer o somatório é maneiro a gente escrever essas forças na forma vetorial.

Olhando para , a orientação dela é dada por um triângulo retângulo. Como o lado do triângulo que tem está paralelo a , para achar a componente da força, a gente multiplica o módulo dela por . E como o lado está paralelo ao eixo , a componente nele é .

Na forma vetorial, temos

Como , temos que

Agora olhando para . A componente em é oposta ao ângulo de e está no sentido negativo de , aí ela fica negativa e o seu valor é o módulo da força vezes seno desse ângulo. Já em , a componente é positiva, e já que ela está coladinha no ângulo, usamos cosseno. Temos:

A força resultante então será a soma desses dois vetores. Vamos somar componente a componente

Assim,

Logo,

Passo 2

Agora precisamos calcular os momentos de cada uma dessas forças com relação ao ponto . Sabemos que o momento de uma força é dado por

Onde é o vetor que sai de (o ponto em relação ao qual queremos o momento) e vai até o ponto de aplicação da força.

Como as duas forças tem o mesmo ponto de aplicação, esses vetores serão iguais para elas. Como o nosso vetor sai de , a origem dos eixos, e vai para o ponto de aplicação da força, o vetor vai ser numericamente igual a coordenada do ponto de aplicação das forças.