Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 7.Problemas - Ex. 63

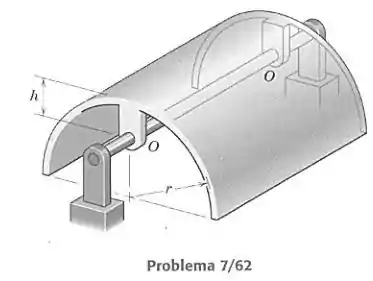
A casca semicilíndrica de raio r gira em torno de um eixo, pelos pontos O , como mostrado. A massa das duas hastes de suporte é pequena comparada à massa da casca. Determine o valor máximo de h para o qual o equilíbrio na posição mostrada é estável.

Passo 1

Se o sistema está em equilíbrio, ao girarmos a casca em torno do eixo de um ângulo pequeno δ θ , devemos ter uma variação da energia potencial do sistema igual a zero:

δ V δ θ = 0

Além disso, se a segunda derivada da função potencial for positiva, o equilíbrio será estável:

δ 2 V δ θ 2 > 0 → E q u i l í b r i o   e s t á v e l

Então, vamos calcular a variação da energia potencial gravitacional relacionada com h , e tentar satisfazer a condição de equilíbrio estável.

Passo 2

A altura do centro de massa da casca cilíndrica é conhecida:

y = 2 π r

Vamos desenhar um giro de ângulo δ θ em torno do eixo:

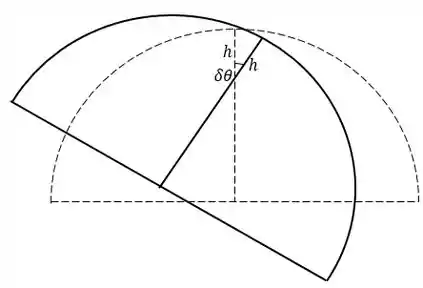
A altura do centro de massa em relação ao eixo de rotação é:

y C - y O = 2 π r - r - h = h - 1 - 2 π r

Então para um giro θ , a altura do centro de massa em relação ao eixo fica:

y = h - 1 - 2 π r cos ⁡ θ

Derivando:

δ y = - h - 1 - 2 π r sen ⁡ θ δ θ

Passo 3

Como temos a variação da altura do centro de massa, temos também a variação da energia potencial gravitacional:

δ V = m g δ h = - m g h - 1 - 2 π r sen ⁡ θ δ θ

Então:

δ V δ θ = - m g h - 1 - 2 π r sen ⁡ θ

No nosso caso temos θ = 0 , então δ V / δ θ já é igual a zero. Falta então que δ 2 V δ θ 2 seja positivo. Derivando de novo:

δ 2 V δ θ 2 = - m g h - 1 - 2 π r cos ⁡ θ > 0

Para θ = 0 o cosseno é 1, temos então:

- m g h - 1 - 2 π r > 0

Cortando m g :

- h + 1 - 2 π r > 0

⇒ h < 1 - 2 π r

⇒ h M á x = 1 - 2 π r

Resposta

h M á x = 1 - 2 π r

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

69- A figura mostra o projeto da seção transversal de uma porta industrial de 35k g , com segmentos articulados, que passa sobre roletes posicionados sobre a guia cilíndrica. Quando a porta está fecha
Substituia a força P agindo na conexão do Prob. 7/17 por um binário M . Determine o momento M do binário necessário para manter o equilíbrio em uma posição arbitrária caracterizada pelo ângulo θ . O m
O torque M , aplicado à conexão leve O A através do eixo O , gira O A de um ângulo θ e eleva a extremidade A da barra uniforme A B de massa m . A extremidade B é sustentada por um pequeno rolete sobre
Determine a força F que a pessoa deve aplicar, tangente ao aro da roda de uma cadeira de rodas, para subir uma rampa inclinada de ângulo θ . A massa combinada da cadeira e da pessoa é m . (Se s é o de
Especifique a força horizontal F necessária para manter o equilíbrio da plataforma de 80 kg em função do ângulo θ feito pelas barras de sustentação em relação à horizontal. Cada uma das três barras un