Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 7.Problemas - Ex. 66

Identifique quais dos itens de ( a ) até ( f ) são mais bem resolvidos ( A ) pelas equações de equilíbrio de força e momento e ( B ) por trabalho virtual. Descreva sucintamente o procedimento para cada solução.

Passo 1

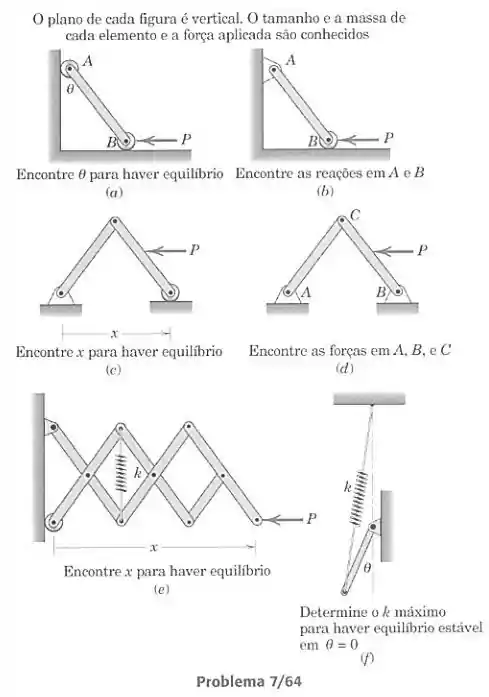
  1. B - Como queremos o valor do ângulo θ , uma medida externa ao sistema, o método do trabalho virtual é mais vantajoso. As forças ativas (que causam trabalho) são o peso da barra e a força P , então calculamos o trabalho virtual infinitesimal realizado pelas duas forças para um giro pequeno δ θ , somamos e igualamos a zero. Resolvemos com apenas uma equação.

    2. Passo 2

  2. A - Dessa vez queremos duas forças que não realizam trabalho para um deslocamento do sistema, e que portanto não aparecem nas equações no método do trabalho virtual. O método da soma das forças e momentos é então mais vantajoso. Isolamos em diagrama de corpo livre a barra e fazemos duas equações de força e uma de momento.

    3. Passo 3

  3. B - Queremos a dimensão x externa ao sistema, entçao podemos usar o método do trabalho virtual. As forças ativas são os pesos das barras e a força P . Calculamos o trabalho virtual realizado pelas duas forças para um pequeno aumento δ x de x , somamos e igualamos a zero. Resolvemos com apenas uma equação.

    4. Passo 4

  4. A - Aqui queremos forças internas ao sistema e que não são todas forças que realizam trabalho, devemos desmembrar os componentes e realizar as equações de força e momento. Isolamos as barras A C e B C em diagrama de corpo livre, e então aplicamos duas equações de força e uma de momento para cada.

    5. Passo 5

  5. B - Como queremos o valor do ângulo x , uma medida externa ao sistema, o método do trabalho virtual é mais vantajoso. As forças ativas (que causam trabalho) são os peso das barra, a força P e a mola, então calculamos o trabalho virtual infinitesimal realizado pelas forças para uma variação pequena δ x de x , somamos e igualamos a zero. Resolvemos com apenas uma equação.

    6. Passo 6

  6. B - Queremos encontrar a constante elástica da mola. Podemos fazer isso pelo princípio do trabalho virtual, encontrando o valor da δ V da variação infinitesimal da energia potencial elástica do sistema para um aumento δ θ do ângulo θ . δ V será função de k . As condições para o equilíbrio estável serão δ V δ θ = 0 e δ 2 V δ θ 2 > 0 . Aplicando as duas, acharemos as restrições para k .

Resposta

a   B

b   A

c   B

d   A

e   B

f   B

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O mecanismo conectado por pinos é restrito em A por um pino e em B por um rolete. P = 50 N, determine o ângulo θ para o equilíbrio. A mola está livre quando θ = 45 º º. Despreze o peso de ambos
Se uma força P = 25 N é aplicada à alça do mecanismo, determine a força que o parafuso exerce sobre a rolha da garrafa. O parafuso está conectado ao pino em A e passa pelo colar que está conectado à b
Determine a força desenvolvida na mola exigida para manter a barra uniforme AB de 50 N ( ≈ 5 kg) em equilíbroo quando θ = 35º
O ‘pantógrafo de Nuremberg’ está sujeito a uma força horizontal P = 600 N. Determine a rigidez k para o equilíbrio quando θ=60º . A mola está livre quando θ=15º.
13- As conexões simétricas sustentam o cilindro de massa m no plano vertical, pela ação dos dois momentos M aplicados a O A e a O B , como mostrado. Determine o valor do momento M em função de θ . A m