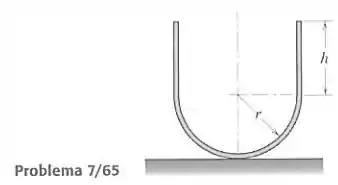
A figura mostra a seção transversal de um recipiente composto por uma casca hemisférica de raio e uma casca cilíndrica de altura , feitas do mesmo material. Especifique o limite de para haver estabilidade na posição vertical quando o recipiente é colocado sobre uma superfície horizontal.

O primeiro passo é determinar as coordenadas do centro de massa da casca. Pela simetria, o centro de massa deve estar no eixo central, e só falta definir a altura. Vamos usar a fórmula do centro de massa da combinação de dois corpos:

Sabe-se que o centro de massa de uma casca hemisférica dica a uma distância do centro. Então:

Além disso a área da casca é:

Para o cilindro, o centro de massa fica no meio:

E sua área é dada por:

Vamos então usar a fórmula:

Dividindo em cima e em baixo por :

Agora vamos desenhar a altura do centro de massa para uma inclinação em relação à vertical:

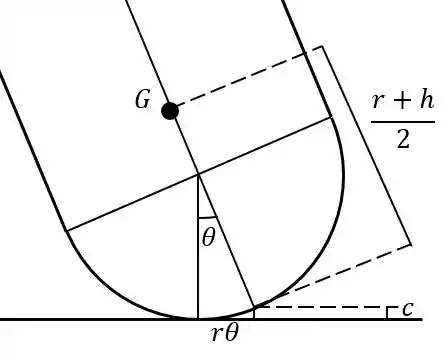
Podemos calcular a pequena altura através da distância na qual a casca gira no chão. O ângulo entre e é , como pode ser observado:

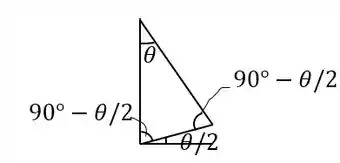
Então:

A altura do centro de massa é então:

Agora vamos obter a expressão da variação da energia potencial gravitacional. A variação da altura do centro de massa em função e é obtida por derivação de :

Então temos a expressão de :

Já temos a derivada da função potencial em função de :

Para , essa função é igual a zero. Queremos agora que a segunda derivada seja positiva. Derivamos de novo:

Para , nossa expressão é reduzida a:

Isso implica que: