Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 3.Problemas - Ex. 49
Determine o peso máximo da caixa, de modo que a tração desenvolvida em qualquer cabo não exceda 2250 N.
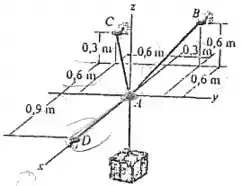
Passo 1
Para encontrar o peso da caixa, sabe-se que deve ser feita a análise de forças do eixo vertical z, já que é o eixo no qual a força peso causada pela caixa tem influência.
Assim, a caixa exerce uma força peso para baixo que pode ser chamada de W.
As outra forças que tem componente no eixo z são e que podem ser denotados na forma vetorial:
Passo 2
Logo, fazendo o diagrama de corpo livre tem-se:
E, então, observando o desenho feito consegue-se montar as equações de equilíbrio.
Passo 3
O equilíbrio requer quer que o somatório de forças em cada dimensão seja nulo, ou seja:
Adotando o sentido dos eixos mostrado no desenho do enunciado:
Passo 4
A partir das equações (1) e (2) é possível obter relações entre as forças, tal que:
Como a tração máxima permitida em cada cabo é de 2250 N, então .
Logo, com esse valor das forças e a equação (3), é possível determinar o máximo peso da caixa:
Logo,
E .