Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 3.Problemas - Ex. 69
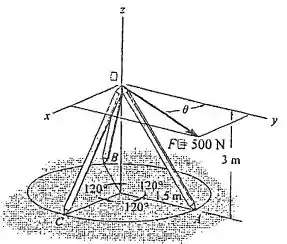
Determine o ângulo tal que seja desenvolvida uma força igual nas pernas OB e OC. Qual é a força em cada perna se a força é direcionada ao longo do eixo de cada uma delas? A força F se localiza no plano x-y. Os suportes em A, B e C podem exercer forças em qualquer direção ao longo das pernas fixadas.
Passo 1
Para encontrar o ângulo, o que deve ser feito primeiramente é o diagrama de corpo livre no qual serão representadas as forças envolvidas.
O enunciado dá a informação de que
Além disso, é possível representar as forças na forma vetorial:
Passo 2
Logo, fazendo o diagrama de corpo livre tem-se:
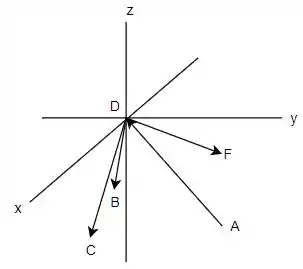
Passo 3
O equilíbrio requer quer que o somatório de forças em cada dimensão seja nulo, ou seja:
Adotando o sentido dos eixos mostrado no desenho do enunciado:
Passo 4
A partir da primeira equação e da condição de que , tem-se que:
E a equação (2) será dada por:
Passo 5
Em seguida, com a nova equação (2) e a equação (3), é possível obter: