Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.10 - Ex. 230
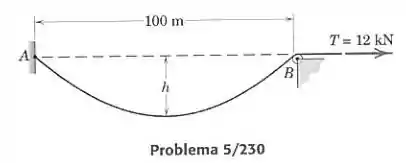
Um cabo, com massa de 15 kg/m, está preso ao ponto A e passa sobre uma pequena polia B, situada sobre a mesma linha horizontal que A. Determine a deflexão e o comprimento do cabo entre e , se uma força de tração de 12 kN for aplicada ao cabo sobre a polia.
Passo 1
Para esse problema primeiro devemos perceber que esse cabo está sob efeito apenas da força peso, que age em cada elemento dependendo do comprimento desse elemento, e da tração. Esse é então um cabo catenário, e tem o formato dado pela seguinte equação:
Escolhendo como origem o ponto mais baixo, temos o ponto pertencendo à curva, então:
Sendo a tração horizontal no ponto mais baixo da corda e a intensidade da força por metro da corda. Outra equação dada pelo livro nos diz que para a corda catenária o tamanho da corda indo da origem até o ponto de coordenada é dado por:
Finalmente, temos a fórmula que relaciona a tração em qualquer ponto da corda de coordenada com a tração que age no ponto mais baixo:
Então devemos achar o valor de utilizando a eq. (3) para a extremidade direita da corda, para então aplicar as fórmulas (1) e (2) para achar e .
Passo 2
Primeiro aplicamos a eq. (3) para achar o valor de . Precisamos do valor de , que é a força peso que a corda sofre por metro de comprimento. Obtemos esse valor multiplicando a densidade linear pela aceleração da gravidade:
Na extremidade da direita temos uma tração , e como a origem é no meio temos . Nossa equação é então:
Resolvendo essa equação com auxílio de um computador, vamos chegar ao valor:
Passo 3
Tendo o valor de , agora usamos a eq. (1) na extremidade da direita, que possui coordenadas :
Passo 4
Agora para achar aplicamos a eq. (2). Vamos calcular da origem até o ponto B, e multiplicar por dois: