Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 3.Problemas - Ex. 5
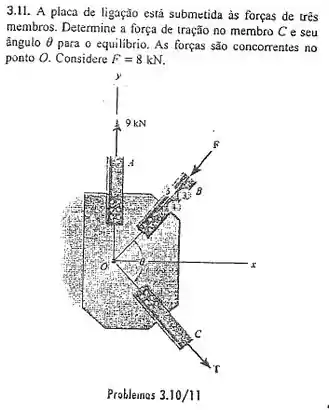
Passo 1
Vamos fazer o diagrama de corpo livre no ponto O:
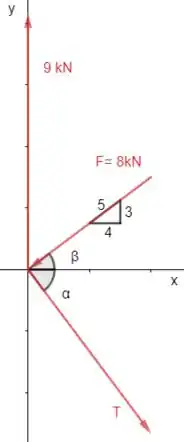
Vamos separar o ângulo em e . E usando as relações trigonométricas podemos descobrir os valores de
Para o ângulo :
Agora falta a gente descobrir , para sabermos o valor de
Passo 2
A soma de forças em e em deve ser zero.
Vamos decompor primeiro as forças em :
Passo 3
Agora vamos decompor as forças em :
Temos o valor dos senos e de :
Seno sobre cosseno é igual a tangente, então:
Então vai ser igual a
Passo 4
Vamos usar a equação que encontramos no Passo 2 para descobrir :
Resposta
Exercícios de Livros Relacionados
28. Para a haste do problema 7.26 , determine a intensidade e a localização do momento fletor máximo:
Oito placas retangulares idênticas de 500 × 750m m , cada qual com massa m = 40k g são mantidas em um plano vertical como mostram as figuras. Todos os apoios consistem em planos sem atrito, roletes ou
Um cursos B de peso W pode mover-se livremente ao longo da haste vertical mostrada na figura. A constante de mola é k , e a mola não fica deformada quando θ = 0 . ( a ) Deduza uma equação em função de
Uma carga vertical P é aplicada na extremidade B de uma haste B C . A constante de mola é k , e a mola não fica deformada quando θ = 90 ° . ( a ) Desprezando o peso da haste, expresse o ângulo θ corre
25. Uma haste de um quarto de círculo de peso W e seção transversal uniforme é apoiada tal como mostra a figura. Determine o momento fletor no ponto J quando θ = 30 ° .