Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 5.Problemas fundamentais - Ex. 10

Determine as reações de apoio nos mancais radiais lisos da tubulação.

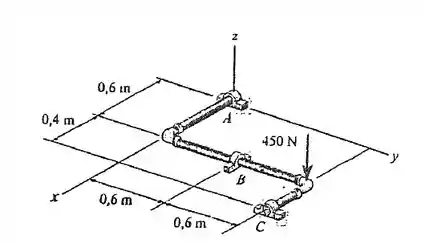
Passo 1

Em toda questão de mecânica geral nós sempre devemos desenhar o diagrama de corpo livre da situação para entendermos quais são as forças e componentes envolvidas. Temos nessa situação as reações de apoio dos mancais em e as duas forças que são aplicadas na barra.

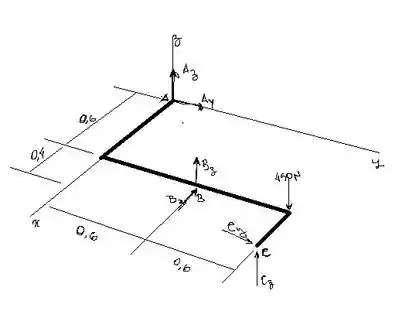
Passo 2

Vamos calcular o momento em relação ao eixo . Para a situação de equilíbrio do sistema, o somatório do momento em relação a um ponto é igual a zero. Assumindo o sentido anti-horário como positivo, temos:

Passo 3

Vamos também olhar o momento em relação ao eixo . Para a situação de equilíbrio do sistema, o somatório do momento em relação a um ponto é igual a zero. Assumindo o sentido anti-horário como positivo, temos:

Temos duas equações e duas icógnitas. Podemos resolver o sistema para encontrar os valores de e ! Assim,

Vamos subtrair a segunda equação da primeira.

Passo 4

Por último, vamos também olhar o momento em relação ao eixo . Para a situação de equilíbrio do sistema, o somatório do momento em relação a um ponto é igual a zero. Assumindo o sentido anti-horário como positivo, temos:

Passo 5

Feita as análises para os momentos, vamos agora analisar o somatório em cada uma das coordenadas. Sabemos que o somatório das forças em , para um sistema em equilíbrio é zero. Assim:

O somatório das forças em , para um sistema em equilíbrio é zero. Logo,

Passo 6

Por último, vamos analisar as forças no eixo . O somatório de forças, em um sistema em equilíbrio, deve ser igual a zero. Portanto, Assumindo a direção para cima como positiva, temos: