Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 9.Problemas fundamentais - Ex. 4
Localize o centro de massa da barra reta se sua massa por unidade de comprimento for dada por .
Passo 1
Fala! Ele nos dá uma barra fina, que a gente pode entender como só tendo como medida significativa o comprimento. Mas ele diz que a massa dela varia ao longo de e pede o centro de massa.
Cara, como essa massa varia ao longo de com essa função diferentona, a gente vai precisar usar a fórmulinha para achar centros de massa que usa integral.
O centro de massa de um corpo tridimensional pode ser calculado da seguinte forma:
Mas como a gente considera que nosso corpo só tem comprimento, só precisamos de
Aí a ideia aqui é montar e calcular essas duas integrais, tá bem? Bora ver como fica!
Passo 2
Precisamos começar achando . Como? Cara, a gente vai escolher um pedacinho bem pequeno da nossa barra, de comprimento , que vamos chamar de elemento diferencial. Esse elemento tem a massa pequena, diferencial, . Olha ele:
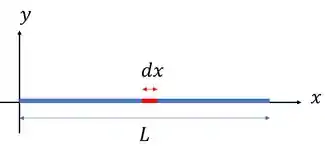
Aí te pergunto: qual é a massa desse carinha? Lembra que ele nos dá a massa por comprimento:
Lembra que massa dividido por volume era densidade em 3D? Para corpos lineares, como o nosso, se a gente divide massa por comprimento, temos uma densidade linear. Então essa expressão que ele nos deu é a densidade linear da barrinha.
E olha que interessante, se a gente multiplicar a densidade linear (quando ela é constante) pelo comprimento, a gente acha a massa! E como é bem pequeno, a gente pode considerar que nossa densidade é constante nesse pedacinho. Aí a massa de é:
Agora é substituir isso nas integrais e partir para o abraço!
Passo 3
Vamos começar pela mais tranquila
O nosso intervalo vai ser intervalo de da barra, ou seja,
Voltando a integral
Passo 4
Agora vamos para a integral que falta
Passo 5
Assim, podemos calcular o valor de !
Resposta
O valor de é: