Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.3 - Ex. 59
A polia transfere um torque constante de para uma bomba por intermédio de seu eixo em . A força trativa no lado de baixo da correia vale . O motor tem uma massa de e gira no sentido horário. Como um dado a ser considerado no projeto, determine o módulo da força no pino de sustentação em .
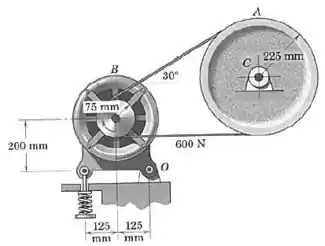
Passo 1
Se o torque gerado pela polia é de , já que sabemos que a força em um dos lados da correia é , podemos calcular a tensão no outro lado:
Precisamos montar alguma equação de equilíbrio que permita calcular alguma componente da força no pino em .
Passo 2
Uma boa forma de fazer isso é analisar o momento em torno de :
E antes de calcular esse momento (justamente para facilitar esse cálculo), vamos substituir a força por um sistema força-binário no centro do motor .
Nesse caso a força continua sendo , mas agindo nesse centro, e precisamos acrescentar um outro momento:
Já que o raio da polia no motor é .
Agora sim, podemos calcular o momento:
E os momentos produzidos pelas forças são os seguintes:
Então o momento total é:
Passo 3
Agora vamos usar outra equação de equilíbrio para calcular a outra componente da força :
E agora podemos calcular o módulo da força:
Resposta
O módulo da força é .