Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 2.Problemas - Ex. 43
Dois cabos estão ligados em e são carregados como mostra a figura. Sabendo que , determine a tração (a) no cabo e (b) no cabo .
Passo 1
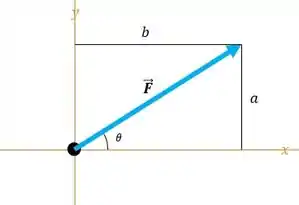
Bom galera, a gente vai encontrar as componentes horizontais e verticais de cada uma das forças que é dada por:
Passo 2
Beleza, o segredo aqui é que o sistema está em equilíbrio, então:
Vamos começar por :
E no eixo , temos:
Passo 3
Por último, a gente só monta um sisteminha de duas equações e resolve:
A gente pode pegar esses valores aí de seno e cosseno na calculadora:
Na primeira equação conseguimos isolar o BC, né:
Daí podemos substituir na segunda equação:
E encontramos:
Resposta
Exercícios de Livros Relacionados
Determine a força normal que a placa A de 500N exerce sobre a placa B de 150N .
Determine as componentes horizontal e vertical da reação do pino A e a força no cabo BC. Despreze a espessura dos membros
A lança do guindaste articulado tem um peso de 625 N e centro de gravidade em G. Se ele suporta uma carga de 3000 N, determine a força que age no pino A e a força no cilindro hidráulico BC quando a la
Um homem fica em pé na ponta do trampolim que é sustentado por duas molas A e B, cada uma com rigidez k = 15 kN/m. Na posição mostrada, o trampolim é horizontal. Se o homem possui uma massa de 40 kg ,
Um instrumento de detecção submarina A está preso ao ponto médio de um cabo de 100 m, suspenso entre dois barcos distando 50 m entre si. Determine a profundidade h do instrumento, que tem massa despre