Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 57
Determine a tração no arame CD logo após o arame AB ser cortado. A pequena esfera tem massa m.
Passo 1
A chave de problemas de cinética está no diagrama de corpo livre. Ao identificarmos todas as forças que o nosso problema está sujeito, conseguiremos visualizar o que há de ser feito mais facilmente.
Relembrando do capítulo de cinemática, vimos que a aceleração centrípeta de um corpo é dada por:
Vamos a questão então!
Passo 2
A nossa bola está sujeita a ação de uma força gravitacional para baixo e de duas forças de tração na direção de cada um dos arames. Entretanto, ao cortarmos um dos arames, eliminámos a força na sua direção. Portanto, obtemos o seguinte diagrama:
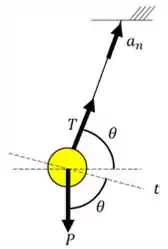
Antes de cortar o arame, a bola está estática. Logo após cortarmos o arame, a mesma contínua estática. Portanto, a sua aceleração normal, que depende da sua velocidade, é nula. Portanto, o somatório de forças na sua direção é igual a 0!!!
Passo 3
Pronto, como foi explicado no Passo 2, o somatório de forças na direção da aceleração normal é igual a 0. Portanto, basta fazermos o somatório de forças nessa direção para descobrirmos a tração no arame CD. Sendo assim, temos: