Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.5 - Ex. 102
Cada pneu no carro de pode suportar uma força de atrito máxima paralela à superfície da estrada de . Esta força limite é aproximadamente constante durante todos os movimentos retilíneos e curvilíneos possíveis do carro e é alcançavel somente se o carro não derrapa. Sob esta frenagem máxima, determine a distância total de parada se os freios são acionados pela primeira vez no ponto quando a velocidade do carro é de e se o carro segue a linha central da estrada.
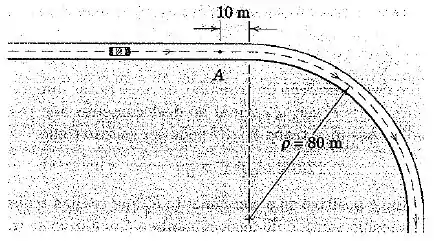
Passo 1
Vamos começar calculando qual é a frenangem máxima. Pela segunda lei de Newton:
Mas essa é a aceleração que cada pneu suporta, para um carro de quatro pneus temos:
E então podemos calcular a velocidade com que o carro “entra” na curva:
Passo 2
A partir do momento que o carro entra na curva temos que considerar a aceleração centrípeta no cálculo da aceleração total sobre os pneus:
E como estamos lidando com frenagem:
E nosso objetivo é saber quanto o carro anda até para parar quando sofre essa desaceleração:
E vamos integrar isso sabendo que a velocidade vai de até , e a distância vai de até um que queremos descobrir:
Passo 3
E agora precisamos calcular essa integral:
E vamos fazer uma substituição:
E agora podemos consultar a tabela de integrais no final do livro:
E então:
E agora é só substituir os valores numéricos:
Resposta
A distância total de parada é .