Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.5 - Ex. 100
Um tubo vazado gira em torno do eixo horizontl que passa pelo ponto com uma velocidade angular constante . Uma partícula de massa é introduzida com velocidade relativa nula em quando e desliza para fora através do tubo liso. Determine como uma função de .
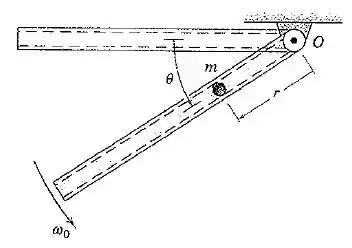
Passo 1
Como estamos interessados no valor de , vamos começar analisando as forças na direção radial:
A única força que age nessa direção é:
Então ficamos com uma equação diferencial ordinária linear não-homogêna de segundo grau.
Passo 2
Você deve se lembrar de que a melhor forma de encontrar uma solução nesse caso é chutar alguma coisa desse tipo:
E vamos substituir isso na equação homogênea (em que simplesmente desconsideramos a constante)
E então:
E agora precisamos buscar a solução não-homogênea:
E aqui não tem jeito, você precisa usar sua experiência e intuição, um bom palpite é:
Supondo que podemos encontrar a constante :
E agora temos que somar a solução particular e a homogênear para encontrar a solução geral:
Passo 3
E agora precisamos achar as constantes usando as condições iniciais:
E isso é um sistema que pode ser resolvido para encontrar e . Da primeira equação podemos obter:
E substituindo na segunda:
E então nossa solução é:
Mas , então:
E temos que lembrar da definição do seno hiperbólico:
Então:
Resolvido!
Resposta
A função é .