Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.5 - Ex. 96
Um helicóptero de combate a incêndio paira sobre um lago enquanto o seu recipiente de água é imerso e cheio. Este em seguida sobe um pouco, tira o recipiente do lago, e começa o seu vôo essencialmente a partir do repouso com uma aceleração horizontal . Obtenha uma expressão para o ãngulo para o qual é máximo. Também determine a tração no cabo como uma função de .
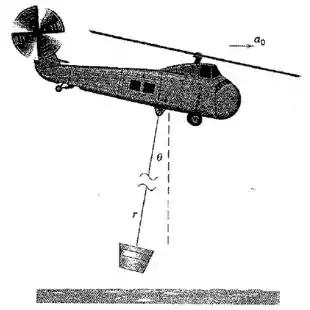
Passo 1
Vamos começar pensando na aceleração tangencial que age sobre o balde. Se estivermos analisando tudo em relação ao helicóptero vamos chegar na seguinte equação:
Onde o sinal negativo aparece porque o peso age no sentido de reduzir o ângulo .
Mas como o helicóptero também tem uma aceleração precisamos adotar um referencial inercial e acrescentar nessa conta. A componente de na direção tangencial é:
E então a nossa soma no referencial inercial é:
Vamos ver o que conseguimos fazer com essa fórmula.
Passo 2
Nosso primeiro objetivo é maximizar a função . Você deve lembrar que um método bastante eficaz de encontrar o máximo de uma função é justamente encontrar os pontos em que sua derivada é zero:
E usando a nossa fórmula de cima:
E esse é o ângulo em que a velocidade angular é máxima (podemos garantir que não é um mínimo porque a derivada segunda é necessariamente negativa).
Passo 3
Vamos analisar as forças na direção do cabo (normal) para encontrar a tração no fio:
E o único termo que não conhecemos nesse fórmula é . Vamos aproveitar a fórmula que descobrimos ali em cima:
E pela regra da cadeia:
Então:
Agora vamos integrar os dois lados, fazendo variar de até um qualquer, e o mesmo para :
Passo 4
Agora vamos substituir isso na equação que tínhamos montado para a tensão no fio:
E agora é só reorganizar um pouco:
Resposta
A velocidade angular é máxima quando e a tração no fio é .