Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.5 - Ex. 97
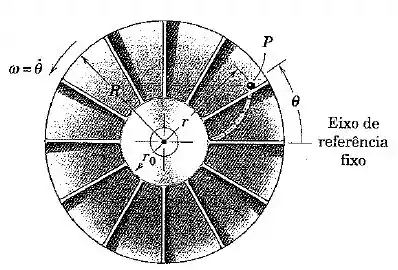
A bomba centrífuga com palhetas radiais lisas gira em torno de seu eixo vertical com uma velocidade angular constante . Encontre o módulo da força exercida por uma palheta sobre uma partícula de massa conforme essa se desloca ao longo da palheta. A partícula é introduzida em sem velocidade radial. Assuma que a partícula tem contato somente com a lateral da palheta.
Passo 1
Primeiro é importante perceber que essa imagem é uma visão de cima, ou seja, o peso da partícula é perpendicular ao plano da página.
Vamos começar analisando as forças na direção radial:
Porque a única força que a centrífuga faz sobre a partícula (a normal) é sempre perpendicular ao raio. E então:
Para as forças na direção tangencial:
Ok, então ficamos com o seguinte sistema:
Passo 2
A primeira equação do sistema é uma equação diferencial ordinária linear homogênea do segundo grau:
Essa é uma equação bastante comum, e você deve lembrar da solução geral para ela:
Eprecisamos achar as constantes através das condições iniciais:
E então a nossa solução é:
E substituindo isso na segunda equação do sistema:
Passo 3
Ainda podemos melhorar um pouco essa fórmula para a força normal:
Retomando a nossa solução para :
E pela relação fundamental:
Agora podemos substituir na equação anterior:
E como podemos disfarçá-lo de para que ele possa entrar naquela raiz quadrada:
Agora sim, resolvido!
Resposta
O módulo da força exercida sobre a partícula .