Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 7.Problemas - Ex. 31

Determine a variação da tensão de cisalhamento na seção transversal de um rebite oco. Qual é a tensão de cisalhamento máxima no rebite? Mostre também que, se r i → r o , então τ m á x = 2 V A

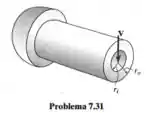
Passo 1

Para resolver essa questão, precisamos ter um raciocínio semelhando ao das questões 7.19 e 7.20.

Começamos olhando a Equação do Cisalhamento:

τ = V Q I t

V e I são constantes. Q é o momento estático e varia dependendo do ponto em que queremos calcular a tensão. Já a base t , no caso de uma circunferência, também é variável. Assim, para encontrar uma equação de cisalhamento que represente uma seção circular, precisaremos calcular as funções que representam Q e t .

Mas observe que a seção é vazada. O momento estático acima da parte vazada se corporta diferente do momento estático que envolve a parte vazada, como mostra a figura abaixo

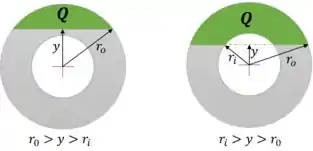
Passo 2

Vamos começar calculando a momento de inércia:

I = π 4 ( r 0 4 - r i 4 )

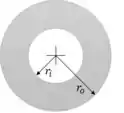
Passo 3

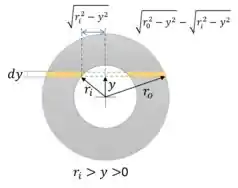
Vamos determinar o momento estático da primeira região. Considere uma “tira” sobre a seção, de espessura infinitesimal d y , a uma distância y do centro e de base t . Com o teorema de pitágoras podemos relacionar a base com o raio e a distância, como mostra a figura abaixo:

t 1 = 2 r 0 2 - y 2

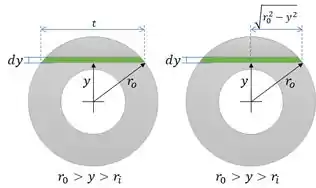
O momento estático de uma tira é:

d Q 1 = t 1 ⋅ d y ⋅ y

Substituíndo o valor de t 1 :

d Q 1 = 2 y ⋅ r 0 2 - y 2 ⋅ d y

O momento estático da região é a soma do momento estático de todas as tiras. Em outras palavras, vamos integrar d Q 1 .

Como queremos uma expressão que represente o momento estático, vamos integrar entre o raio máximo e um ponto y qualquer. Lembre que estamos trabalhando na região r 0 > y > r i :

Q 1 = ∫ y r 0 2 y ⋅ r 0 2 - y 2 ⋅ d y

Q 1 = - 2 3 r 0 2 - y 2 3 / 2 y r 0

Q 1 = 2 3 r 0 2 - y 2 3 / 2

Perceba que quando y = r i

Q 1 r i = 2 3 r 0 2 - r i 2 3 / 2

Passo 4

Vamos fazer o mesmo processo para a região onde há o furo, r i > y > 0 . Observe que devido a região vazada, o valor da base t muda.

t 2 = 2 r 0 2 - y 2 - r i 2 - y 2

O momento estático de uma tira é:

d Q 2 = t 2 ⋅ d y ⋅ y

Substituíndo o valor de t 2 :

d Q 2 = 2 y r 0 2 - y 2 - r i 2 - y 2 ⋅ d y

Perceba que o momento estático desse região é determinado pela soma integral das tiras mais o momento estático da seção anterior, como mostra a figura abaixo:

Q 2 = Q 1 ( r i ) + ∫ A d Q 2

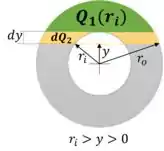
Lembre que estamos trabalhando na região r i > y > 0 :

Q 2 = Q 1 ( r i ) + ∫ y r i 2 y ⋅ r 0 2 - y 2 - r i 2 - y 2 ⋅ d y

Simplificando a integral:

Q 2 = Q 1 ( r i ) + ∫ y r i 2 y ⋅ r 0 2 - y 2 ⋅ d y - ∫ y r i 2 y ⋅ r i 2 - y 2 ⋅ d y

Aplicando a integração:

Q 2 = Q 1 ( r i ) - 2 3 r 0 2 - y 2 3 / 2 y r i + 2 3 r i 2 - y 2 3 / 2 y r i

Aplicando os valores:

Q 2 = 2 3 r 0 2 - r i 2 3 / 2 - 2 3 r 0 2 - r i 2 3 / 2 + 2 3 r 0 2 - y 2 3 / 2 + 2 3 r i 2 - r i 2 3 / 2 - 2 3 r i 2 - y 2 3 / 2

Chegamos na expressão:

Q 2 = 2 3 r 0 2 - y 2 3 / 2 - r i 2 - y 2 3 / 2

Passo 5

Vamos aplicar na equação de cisalhamento

Para a primeira região r 0 > y > r i :

τ 1 = V Q 1 t 1 I

Substituindo o Q 1 , t 1 e I

τ 1 = V π 4 ( r 0 4 - r i 4 ) ⋅ 2 3 r 0 2 - y 2 3 / 2 2 r 0 2 - y 2

Simplificando:

τ 1 = 4 V 3 π ⋅ r 0 2 - y 2 r 0 4 - r i 4

Passo 6

Para a segunda região r i > y > 0 :

  τ 2 = V Q 2 t 2 I

Substituindo o Q 2 , t 2 e I :

τ 2 = V ⋅ 2 3 r 0 2 - y 2 3 / 2 - r i 2 - y 2 3 / 2 π 4 r 0 4 - r i 4 ⋅ 2 r 0 2 - y 2 - r i 2 - y 2

Simplificando:

τ 2 = 4 V 3 π ⋅ r 0 2 - y 2 3 / 2 - r i 2 - y 2 3 / 2 r 0 4 - r i 4 ⋅ r 0 2 - y 2 - r i 2 - y 2

Passo 7

Vamos agora descobrir a tensão máxima.

Perceba que quando y = 0 , a base t 2 será a menor possível e o momento estático será o maior possível. Por consequência, quando y = 0 a tensão será máxima:

y = 0 ⇒ τ 2 = 4 V 3 π ⋅ r 0 3 - r i 3 r 0 4 - r i 4 ⋅ r 0 - r i

Podemos simplificar a expressão usando o produto notável: a 3 - b 3 = ( a 2 + a b + b 2 ) ( a - b )

τ 2 = 4 V 3 π ⋅ ( r 0 2 + r 0 r i + r i 2 ) r 0 - r i r 0 4 - r i 4 ⋅ r 0 - r i

Chegamos no valor máximo:

τ 2 = 4 V 3 π ⋅ ( r 0 2 + r 0 r i + r i 2 ) r 0 4 - r i 4

Passo 8

Pra finalizar, vamos considerar a situação: r i → r 0

lim r i → r 0 ⁡ τ = lim r i → r 0 ⁡ 4 V 3 π ⋅ ( r 0 2 + r 0 r i + r i 2 ) r 0 4 - r i 4

Podemos simplicar mais utilizando outro produto notável: a 4 - b 4 = ( a 2 + b 2 ) ( a 2 - b 2 )

lim r i → r 0 ⁡ τ = lim r i → r 0 ⁡ 4 V 3 π ⋅ ( r 0 2 + r 0 r i + r i 2 ) r 0 2 + r i 2 r 0 2 - r i 2

Se reorganizarmos:

lim r i → r 0 ⁡ τ = lim r i → r 0 ⁡ 4 V 3 ⋅ 1 π r 0 2 - r i 2 ⋅ ( r 0 2 + r 0 r i + r i 2 ) r 0 2 + r i 2

Perceba que π r 0 2 - r i 2 é igual a área A da seção:

lim r i → r 0 ⁡ τ = lim r i → r 0 ⁡ 4 V 3 ⋅ 1 A ⋅ ( r 0 2 + r 0 r i + r i 2 ) r 0 2 + r i 2

Tirando as constantes do limite:

lim r i → r 0 ⁡ τ = 4 V 3 A lim r i → r 0 ⁡ ( r 0 2 + r 0 r i + r i 2 ) r 0 2 + r i 2

Efetuando o limite:

τ = 4 V 3 A ⋅ ⁡ ( r 0 2 + r 0 2 + r 0 2 ) r 0 2 + r 0 2

Chegamos no resultado:

τ = 2 V A

Resposta

Tensão máxima: τ 2 = 4 V 3 π ⋅ ( r 0 2 + r 0 r i + r i 2 ) r 0 4 - r i 4

Tensão limite: τ = 2 V A

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O tubo está sujeito a uma força de cisalhamento V = 40k N . Determine o fluxo de cisalhamento no tubo nos pontos A e B
A viga é composta por quatro chapas e está sujeita a uma força de cisalhamento V = 25k N . Determine o fluxo de cisalhamento máximo na seção transversal.
A escora de alumínio tem 10 m m de espessura e a seção transversal mostrada na figura. Se for submetida a um cisalhamento V = 150N , determine o fluxo de cisalhamento máximo na escora.
A cantoneira está sujeita a um cisalhamento V = 10k N . Faça um rascunho da distribuição do fluxo de cisalhamento ao longo da aba AB. Indique valores numéricos em todos os picos.
A força de cisalhamento V = 18 k N é aplicada à viga-mestra-caixão. Determine a posição d das chapas de reforço B E e F G de modo que o fluxo de cisalhamento em A seja duas vezes maior do que o fluxo