Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 14.Problemas - Ex. 44

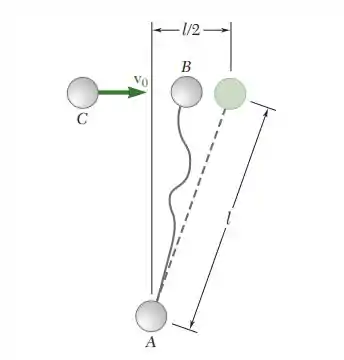
14.44. Três esferas, cada uma de massa m, podem deslizar livremente sobre uma superfície horizontal sem atrito. As esferas A e B estão ligadas por um fio inextensível e inelástico de comprimento l e em repouso na posição mostrada na figura quando a esfera B é atingida perpendicularmente pela esfera C, que se move para direita com uma velocidade v0. Sabendo que o fio não está esticado quando a esfera B é atingida pela esfera C e considerando que o choque entre B e C é perfeitamente elástico, determine (a) a velocidade de cada esfera imediatamente após o fio ficar esticado e (b) a fração da energia cinética inicial do sistema que é dissipada quando o fio é esticado.

Passo 1

Vamos para mais uma questão!

A gente pode separar esse problema em dois movimentos, o primeiro movimento termina quando a bola C atinge a bola B.

A primeira coisa que precisamos é perceber que o momento linear é conservado nesse movimento, então

∑ L i = ∑ L f

O que significa

m v 0 = m v C + m v B 1

A gente pode cortar as massas

v 0 = v C + v B 1                           ( I )

A colisão é perfeitamente elástica, como o exercício diz, então a energia é conservada, o que significa que podemos escrever

1 2 m v 0 2 = 1 2 m v C 2 + 1 2 m v B 1 2

A gente pode cortar m 2

v 0 2 = v C 2 + v B 1 2               ( I I )

Olha só, a gente pode elevar a equação (I) ao quadrado e substituir na equação (II)

v C + v B 1 2 = v c 2 + v B 1 2

Passo 2

Olha só, a gente pode elevar a equação (I) ao quadrado e substituir na equação (II)

v C + v B 1 2 = v c 2 + v B 1 2

Vamos expandir esse quadrado

v C 2 + v B 1 2 + 2 v c v B 1 = v C 2 + v B 1 2

Isso fica

2 v c v B 1 = 0

Então v C ou v B 1 é nulo. Bom, não faz sentido físico a bola C atingir a bola B e a bola B ficar parada sendo que a massa das duas bolas é a mesma, logo a única solução possível para isso é

v C = 0

Se a gente substituir esse valor na equação (I) vamos chegar num resultado interessante

v 0 = v C + v B 1

v 0 = 0 + v B 1

v 0 = v B 1

Olha que interessante! A bola C transferiu toda energia para bola B.

Passo 3

Vamos para o segundo movimento, agora o movimento acaba quando a corda que liga a bola A com a bola B está completamente esticada.

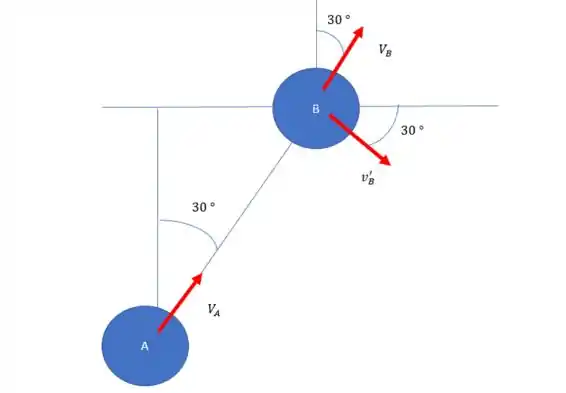
A corda é inextensível, então ao final do movimento, a velocidade da bola B na direção da corda que liga as duas bolas tem que ser igual a velocidade da corda A. Isso não significa que a velocidade total da bola B é igual ao da bola A, ainda existe uma componente perpendicular da velocidade na bola B. Olha o desenho:

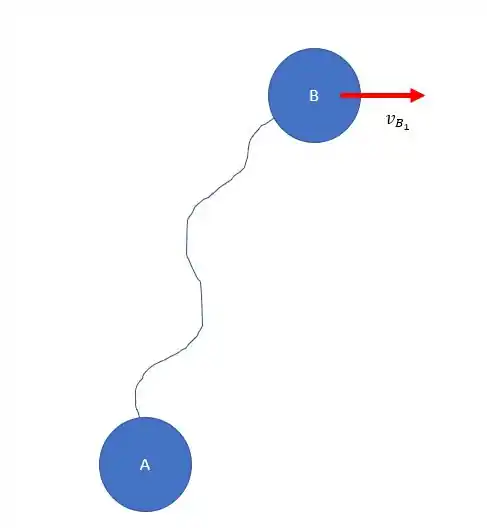
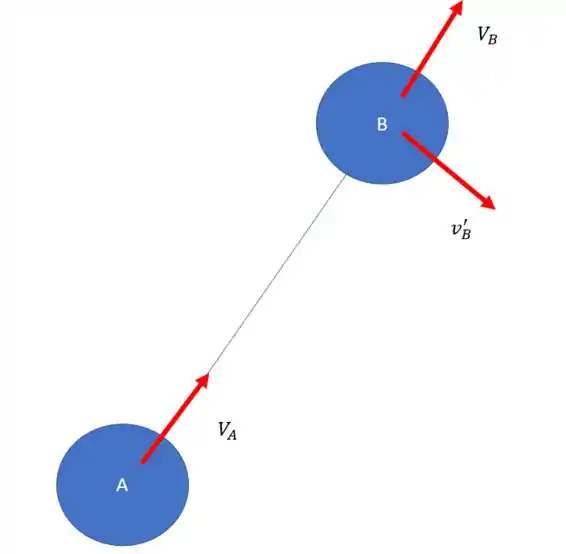
Se a gente olha pra imagem de novo a gente consegue até determinar os ângulos, repare na imagem do problema, a gente pode tirar o seguinte triangulo.

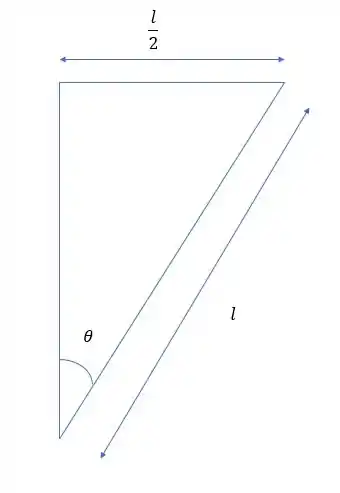
A gente pode determinar esse ângulo, a gente sabe o cateto oposto e a hipotenusa, então a gente sabe o seno

sin ⁡ θ = l 2 l = 1 2

Então

θ = arcsin ⁡ 1 2 = 30   °

Então temos

Passo 4

A gente fez tudo isso para poder calcular o momento para cada componente, assim fica mais fácil para a gente.

Na componente y , fica o seguinte

0 = m v A cos ⁡ 30 ° + m v B cos ⁡ 30 ° - m v B ' sin ⁡ 30   °

Mas como a gente determinou

v A = v B

Então

0 = 2 m v A cos ⁡ 30 ° - m v B ' sin ⁡ 30   °

A gente pode cortar as massas

0 = 2 v A cos ⁡ 30 ° - v B ' sin ⁡ 30   °

Vamos isolar v B '

v B ' = 2 v A cos ⁡ 30 ° sin ⁡ 30 ° = 2 3   v A

E para a componente x temos

m v 0 = m v A sin ⁡ 30 ° + m v B sin ⁡ 30 ° + m v B ' cos ⁡ 30 °

Isso vai ficar

m v 0 = 2 m v A sin ⁡ 30 ° + m v B ' cos ⁡ 30 °

Podemos cortar a massa

v 0 = 2 v A sin ⁡ 30 ° + v B ' cos ⁡ 30 °

Vamos substituir v B '

v 0 = 2 v A sin ⁡ 30 ° + 2 3   v A cos ⁡ 30 °

Agora a gente pode chegar numa expressão para v A

v 0 = v A 1 + 3

Então

v A = v 0 4

Passo 5

Agora a gente pode determinar todas as velocidades, veja

v B = v A   i ^ + v B '   j ^

Mas

v B ' = 2 3   v A = 2 3   v 0 4 = 3 2 v 0

Logo

v B = v 0 4   i ^ + 3 2 v 0   j ^

E o módulo é

v B ' = v 0 4 2   + 3 2 v 0 2

E

v C = 0

Passo 6

Agora vamos para o item (b). Para faze-lo a gente só precisa fazer a energia inicial, a final, e ver a diferença entre as duas.

T i = 1 2 m v 0 2

E

T f = 1 2 m v A 2 + v B 2 + v C 2

Vamos substituir com os valores que encontramos

T f = 1 2 m v 0 4 2 + v 0 4 2   + 3 2 v 0 2 2 + 0 2

Então

E p e r d i d a = T i - T f

E p e r d i d a = 1 2 m v 0 2 - 1 2 m v 0 4 2 + v 0 4 2   + 3 2 v 0 2 2 + 0 2

Podemos cortar 1 2   m

E p e r d i d a = v 0 2 - v 0 4 2 - v 0 4 2   + 3 2 v 0 2 2

Isso fica

E p e r d i d a = v 0 2 - v 0 2 16 - v 0 2 16 + 3 4 v 0 2

Então

E p e r d i d a = v 0 2 1 - 1 16 - 1 16 - 3 4 = 1 8   v 0 2

Resposta

a)

v A = v 0 4   i ^ v B = v 0 4   i ^ + 3 2 v 0   j ^ v C = 0

b)

E p e r d i d a = 1 8 v 0 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma espaçonave que descreve uma órbita circular em torno da Terra a uma velocidade de 24 × 10 3k m / h libera sua cápsula frontal de 600k g de massa bruta que inclui 400k g de combustível. Sabendo que
Um satélite de comunicação de 50k N , incluindo o combustível, foi ejetado do ônibus espacial descrevendo uma órbita circular de baixa altitude em torno da terra. Depois que o satélite foi lentamente
Uma corrente de comprimento l e massa m cai por meio de um pequeno buraco existente em uma placa. Inicialmente, quando y é muito pequeno, a corrente está em repouso. Em cada um dos casos apresentados,
No experimento de dispersão de partículas feito no Problema 14.24, sabe-se que a partícula alfa é lançada a partir de A 0( 300 ,0 ,300 ) e que ela colide com o núcleo de oxigênio C em Q( 240 ,200 ,100
Em um jogo de bilhar, a bola A se desloca com uma velocidade v 0 = v 0 i quando ela atinge as bolas B e C , que estão em repouso uma ao lado da outra. Considerando as superfícies sem atrito e um choqu