Determine a velocidade angular e acelaração angular da placa CD do mecanismo triturador de pedras no instante em que AB está na horizontal. Neste instante, = e = . O membro de acionamento AB está girando cm uma velocidade angular constante = 4 rad/s.
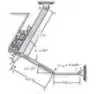
Passo 1
Como visto na teoria, sabemos que , então, podemos calcular .
Passo 2
Agora que calculamos podemos calcular . Mas para ajudar a gente nesse cálculo, vamos observar a figura abaixo.
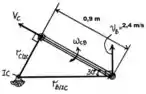
Nela podemos observar que . Então:
Ainda com a ajuda da figura, conseguimos perceber que , com isso:
Passo 3
Para finalizar essa primeira parte da questão, vamos calcular
Passo 4
Terminamos a primeira parte do exercício, ufa! Vamos iniciar a segunda parte, ou seja, calcularemos o valor de . Para isso, iremos tomar como base a figura abaixo:
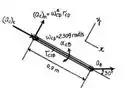
Na figura acima já podemos observar que foi colocado os pares ordenados. Inicialmente, vamos calcular o valor de . Como não há aceleração tangencial, ou seja, somente normal, podemos calculá-la por .
Passo 5
Chegamos em um ponto que parece óbvio, mas tome cuidado com o óbvio! Temos que garantir que ambos os lados da viga possuam o mesmo valor de aceleração, isto é,
Vamos substituir os valores que já conhecemos na equação acima:
Temos que garantir que as coordenadas e sejam iguais, então:
Eixo : .
Eixo : .
Então,