Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas - Ex. 137

A bola C se desloca com uma velocidade de 3 m/s, que está aumentando a uma taxa constante de 1,5 m/s2, ambas medidas em relação à placa circular e direcionadas como mostrado. No mesmo instante, a placa gira com a velocidade angular e a aceleração angular mostradas. Determine a velocidade e a aceleraão da bola nesse instante.

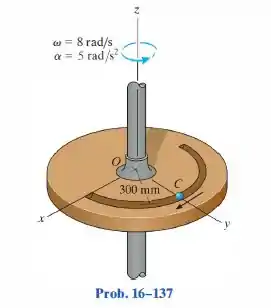
Passo 1

Para a resolução desse exercício, iremos utilizar a análise do movimento relativo usando um sistema de eixos em rotação. O eixo de rotação de referência x y z está coincidindo com o eixo X Y Z , como mostra a figura abaixo:

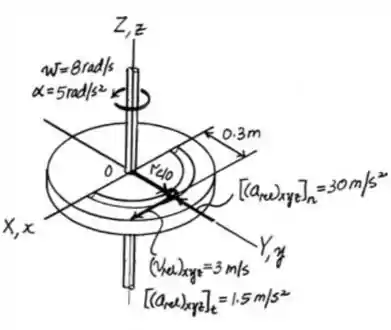
Analisando a figura, temos:

v O = a o = 0 ω = 8 k   r a d / s α = 5 k   r a d / s 2

Passo 2

Ainda de acordo com a figura do Passo 1, vamos calcular tanto o vetor posição r C / O assim como velocidade relativa (dado no enunciado).

r C / O = [ 0,3 j ]   m

v r e l x y z = 3 i   m / s

De acordo com o enunciado, a aceleração relativa tangencial é a r e l x y z = 1,5 i   m / s 2 . Basta encontrarmos a aceleração normal, isto é, a r e l x y z n = v r e l x y z 2 r C / O = 3 2 0,3 = 30   m / s 2 . Então,

a r e l x y z = 1,5 i - 30 j   m / s 2

Passo 3

Para calcular a velocidade em C, vamos usar a fórmula abaixo:

v C = v O + ω × r C / O + v r e l x y z

Agora que já sabemos que fórmula iremos utilizar, vamos substituir na equação acima os valores que já temos. Então,

v C = 0 + 8 k × 0,3 j + 3 i =   0,6 i   m / s

Passo 4

Agora que conseguimos encontrar o valor da velocidade, basta encontrarmos o valor da aceleração. Para isso, utilizaremos a fórmula abaixo:

a C = a O + ω ˙ × r C / O + ω × ω × r C / O + 2 ω × v r e l x y z + a r e l x y z

a C = 0 + 5 k × 0,3 j + 8 k × 8 k × 0,3 j + 2 . 8 k × 3 i + 1,5 i - 30 j

a C =   - 1,2 j   m / s 2

Resposta

v c = 0,6 i   m / s

a c = - 1,2 j   m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

16.97. A unidade de bombeamento de petróleo consiste de um balancim A B , a barra de conexão B C e a manivela C D . Se a manivela gira com uma taxa constante de 6 r a d / s , determine a velocidade da
Os componentes do dispositivo de comutação do prob. 5/85 são mostrados novamente aqui. Se a velocidade v da haste de controle é de 0,9 m/s e está diminuindo na taxa de 6 m/s² quando θ = 60 ° , determi
Se a extremidade A da barra restrita possui uma velocidade constante para eixo v A de 2 m/s quando a barra passa pela posição para qual θ = 30 ° , determine a aceleração do centro de massa G no meio d
O movimento da barra ABC é controlado pelo movimento horizontal da haste do pistão do cilindro hidráulico D e pela guia vertical para o cursor articulado em B. Para o instante em que θ = 45 ° , a hast
Um mecanismo de avanço intermitente para fita perfurada F consiste no elemento DAB acionado pela manivela OB. O traçado do movimento do dente D é indicado pela linha tracejada. Determine o módulo da a