Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.8 - Ex. 196
O pino A no cotovelo AOD é guiado pelos frisos do cursor B, que desliza com uma velocidade constante de 0,9 m/s ao longo do eixo fixo durante um intervalo do movimento. Para a posição determine a aceleração do embolo CE, cuja extremidade superior é posicionada pela ranhura radial no cotovelo.
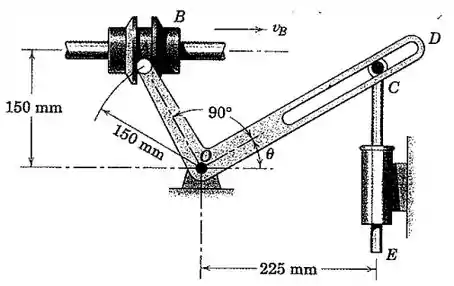
Passo 1
Bom pessoal, quando temos uma questão com deslizamento em ranhuras, pegamos um ponto P pertencente ao elemento ranhurado que coincide com o ponto C do pistão. Assim, temos dois pontos com diferentes velocidades e a velocidade relativa entre estes pontos deve estar na direção da ranhura.
Vamos fazer um esboço do mecanismo representando seus vetores velocidade:
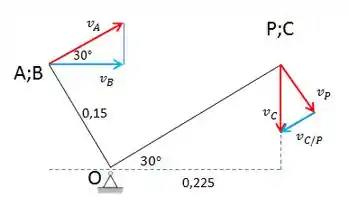
Beleza! Vamos agora calcular a velocidade angular de AOD:
Também podemos calcular a velocidade do ponto P:
Pelo triângulo formado pelos vetores
Passo 2
Agora, vamos para o cálculo das acelerações.
A aceleração do ponto A pode ser representada por:
Onde:
O ponto possui velocidade constante na direção horizontal. Desta forma, sua resultante deve estar na vertical, ou seja, as componentes da normal e tangencial na direção x devem se anular. Vamos representar os vetores em um diagrama:
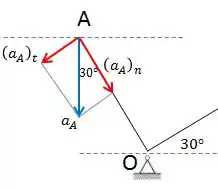
Então, projetando em x, temos que:
Agora, vamos calcular a aceleração do ponto P:
Onde:
Bom, agora vamos usar a equação da aceleração entre P e C:
Como P e C possuem a mesma coordenada,
Onde:
Beleza, agora vamos visualizar os vetores!
A aceleração relativa entre P e C deve ter a direção da ranhura, da mesma forma que a velocidade relativa.
Já a aceleração do ponto C deve seguir o movimento do pistão, estando, portanto na vertical.
Usando a regra da mão direita em , vemos que sua direção e sentido são os mesmos de .
Vamos desenhar um diagrama para visualizar melhor:
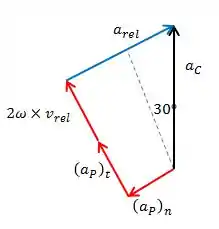
Então, a aceleração de C pode ser achada por: