Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 18.Problemas - Ex. 22

Determine a velocidade angular das duas barras de 10 kg quando θ = 9 0 ° , se elas são liberadas do repouso na posição θ = 60 ° . Despreze o atrito.

Passo 1

Devido a simetria do sistema em estudo, sabemos que a velocidade angular do braço AB e do braço BC serão iguais a ω , com isso, como os braços possuem a mesma medida, eles também terão a mesma velocidade linear de seu centro de massa:

v G = ω r G = ω ( 1,5 )

Agora iremos calcular o momento de inércia de cada barra em relação ao seu centro de massa:

I G = 1 12 m l 2 = 1 12 10 3 2 → I G = 7,5   k g . m 2

Sendo assim, a energia cinética final do sistema é dada por:

T 2 = 2 1 2 I G ω 2 + 1 2 m v G 2 = 2 1 2 7,5 ω 2 + 1 2 10 ω 1,5 2

T 2 = 30 ω 2

Passo 2

Como o sistema está inicialmente em repouso, T 1 = 0 . Através da analise da figura a seguir:

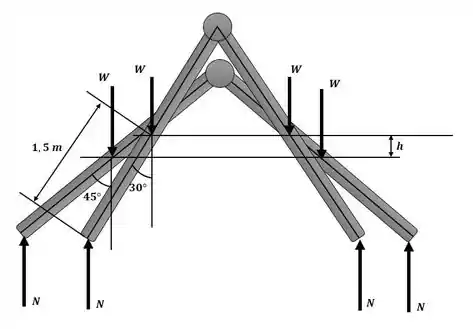
Sabemos que N não realiza trabalho, equanto N realiza. Sendo assim, quando θ = 90 ° , W se desloca de:

h = 1,5 c o s 30 ° - 1,5 c o s 45 ° = 0,2384   m

Sendo assim, o trabalho realizado pelo peso W é dado por:

U W = W h = 10 9,81 0,2384 → U W = 23,38   J

Passo 3

Agora iremos aplicar o princípio do trabalho e da energia:

T 1 + ∑ U 1 - 2 = T 2

0 + 2 ( 23,38 ) = 30 ω 2

ω = 1,25   r a d / s

Resposta

ω = 1,25   r a d / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Quando o motorista aciona os freios de uma camioneta se deslocando a 10 km/h, ela derrapa 3 m antes de parar. Qual a distância que a camioneta vai derrapar se ela estiver se deslocando a 80 km/h quand
A mola na arma de brinquedo tem um comprimento não deformado de 100 mm. Ela está comprimida e travada na posição mostrada. Quando o gatilho é puxado, a mola se distende 12,5 mm, e a bala de 20 g se de
O tampão liso tem massa de 10 kg e é empurrado contra uma série de molas prato Belleville de maneira que a compressão na mola é s = 0,015m . Se a força da mola sobre o tampão é F = ( 4,5s 1 / 3 )N , o
As molas A B e C D têm rigidez k = 300N / m e k ' = 200N / m , respectivamente, e as duas molas têm comprimento não deformado de 600 mm. Se o anel liso de 2 kg parte do repouso quando as molas não est
O carro de 2 Mg tem velocidade v 1 = 100k m / h quando o motorista vê um obstáculo na frente do carro. Se leva 0,75 s para ele reagir e travar os freios completamente, fazendo com que o carro derrape,