Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 18.Problemas - Ex. 17

A tampa da caixa de 6 kg é mantida em equilíbrio pela mola torsional em θ = 60 ° . Se a tampa é forçada a fechar-se, θ = 0 ° , e em seguida é liberada, determine sua velocidade angular no instante em que se abre em θ = 45 ° .

Passo 1

Começaremos o exercício escrevendo o momento que atua sobre a tampa com base no ângulo inicial da mola torsional:

M = k θ 0 = 20 θ 0

Agora, com o auxílio do diagrama a seguir, podemos escrever o somatório de momento com relação ao ponto C:

+ ↺ ∑ M C = 0

6 9,81 c o s 60 ° 0,3 - 20 θ 0 = 0

θ 0 = 0,4414   r a d

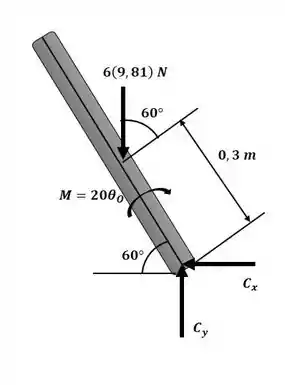
Temos ainda que o momento de inércia da tampa é dada por:

I C = 1 3 m b 2 = 1 3 6 0,6 2 → I C = 0,72   k g . m 2

Sendo assim, sua energia cinética é dada por:

T = 1 2 I C ω 2 = 1 2 0,72 ω 2 → T = 0,36 ω 2

Passo 2

Como a tampa está inicialmente em repouso, T 1 = 0 . Através da analise da figura a seguir:

Sabemos que C x ,     C y não exercem trabalho sobre o sistema, enquanto M e os pesos exercem. Quando θ = 0 ° e θ = 45 ° , os ângulos de rotação da mola são:

θ 1 = 1,489   r a d

θ 2 = 1,489 - π 4 → θ 2 = 0,703   r a d

Temos que notar ainda que, quando θ = 45 ° o peso da tampa está a uma distância h = 0,3 s e n 45 ° = 0,2121   m . Sendo assim, os trabalhos realizados por M e pelo peso são dados por:

U M = ∫ M d θ = ∫ θ 2 θ 1 20 θ d θ = 10 θ 2 0,7032 1,4886 → U M = 17,22   J

U W = - W h = - 6 9,81 0,2121 → U W = - 12,49   J

Passo 3

Agora iremos aplicar o princípio do trabalho e da energia:

T 1 + ∑ U 1 - 2 = T 2

0 + 17,22 + - 12,49 = 0,36 ω 2

ω = 3,62   r a d / s

Resposta

ω = 3,62   r a d / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

3/138) O jogo de duas molas é usado para trazer o êmbolo A de 0,5k g para o repouso a partir de uma velocidade de 5 m / s e inverrter o seu sentido de movimento . A mola internaaumenta a desaceleração
3/140) O cilindro de 6k g é liberado a partir do repouso na posição mostrada e cai sobre a mola , que foi inicialmente pré-comprimida em 50m m pela trava leve e fios restritivos . Se a rigidez da mola
3/142) Ensaios extensivos de um automóvel experimental de 900k g revelaram a força de arrasto aerodinâmico F A e a força total não aerodinâmica de resistência ao rolamento F R serem como mostrado no g
O carro de massa m acelera em uma estrada horizontal sob a ação da força motriz F de uma velocidade v 1 até uma velocidade mais alta v 2 em uma distância s . Se o motor desenvolve uma potência de saíd
O bloco de 10k g é liberado a partir do repouso sobre a superfície no ponto B , onde a mola foi esticada por uma distância de 0,5m a partir de sua posição neutra A . O coeficiente de atrito dinâmico e