Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 14.Problemas - Ex. 3
O tampão liso tem massa de 10 kg e é empurrado contra uma série de molas prato Belleville de maneira que a compressão na mola é . Se a força da mola sobre o tampão é , onde é dada em metros, determine a velocidade do tampão após ele se afastar da mola. Despreze o atrito.
Passo 1
O enunciado nos dá as seguintes informações:
Massa do tampão: ;
Compressão na mola: ;
Força da mola sobre o tampão:
Devemos determinar a velocidade do tampão após ele se afastar da mola.
Primeiramente, desenhamos o diagrama de corpo livre do tampão:
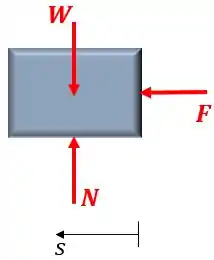
Onde é a força peso, é a aceleração da gravidade, é aforça normal e é a força exercida pela mola.
Vamos dividir a situação em instante (1), onde a mola foi comprimida e a velocidade do tampão é igual à zero nesse mometo. No instante (2), a mola é solta e empurra o tampão.
Passo 2
Vamos aplicar o Princípio de Trabalho e Energia:
Onde
Neste caso, o trabalho possui valor positivo, pois a força possui a mesma direção do deslocamento.
Substituindo estes valores na equação principal, obtemos