Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 14.Problemas - Ex. 8
A mola na arma de brinquedo tem um comprimento não deformado de 100 mm. Ela está comprimida e travada na posição mostrada. Quando o gatilho é puxado, a mola se distende 12,5 mm, e a bala de 20 g se desloca ao longo do cano. Determine a velocidade da bala quando ela deixa a arma. Despreze o atrito.
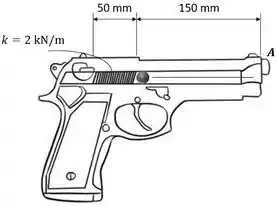
Passo 1
O enunciado nos dá as seguintes informações:
Comprimento não deformado da mola: ;
Constante el[astica da mola: ;
Massa da bala:
Dedemos determinar a velocidade da bala ao deixar a arma no ponto .
Inicialmente, desenhamos o diagrama de corpo livre da bala:
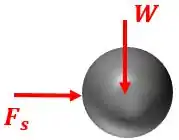
Onde é a força peso e é a força exercida pela mola.
Além disso, vemos que a bala se deslocará somente na horizontal enquanto estiver dentro do cano da arma de brinquedo.
Passo 2
Agora, vamos analizar a mola.
Sabemos que seu comprimento inicial .
Antes do gatilho ser acionado, seu comprimemento é de
Logo, no primeiro momento, .
Após o acionamento do gatinho, a mola irá se distender 12,55 mm. Portanto,
E a deformação da mola no segundo momento será de .
Resumindo:
Passo 3
Agora, utilizaremos o Princípio do Trabalho e Energia para encontrar a velocidade da bala ao sair do cano da arma de brinquedo.
Na direção do movimento da bala, só temos a ação da força elástica. Portanto, esta será a força que realiazará trabalho sobre a bala e este trabalho será positivo, pois atua na mesma direção e sentido de . O trabalho de uma mola é dado por
Temos que
Sabemos que no instante (1), a bala está parada e no instante (2) a mola terá velocidade . Logo,
Substituindo esses valores na equação principal, obtemos