Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.2 - Ex. 28

Uma motocicleta parte do repouso com uma aceleração inicial de 3 m / s 2 e a aceleração então varia com a distância s como mostrado na figura. Determine a velocidade v da motocicleta quando s = 200   m . Determine também o valor da derivada d v / d s neste ponto.

Passo 1

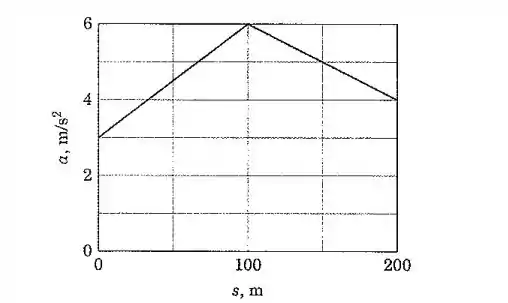
Bom, temos um gráfico da aceleração a em função da posição s . Precisamos de alguma equação que relacione as duas grandezas:

a = d v d t

d v d t = d v d s   d s d t = v d v d s

a = v d v d s

a   d s = v   d v

E se integrarmos os dois lados dessa equação, o termo da esquerda vai dar a área sob o gráfico do enunciado:

∫ 0 s a   d s = ∫ 0 v v   d v

E como a motocicleta parte do repouso:

1 2 v 2 = ∫ 0 s a   d s

Passo 2

Para descobrir a velocidade da motocicleta quando s = 200   m , podemos substituir:

1 2 v 2 = ∫ 0 200 a   d s

Calculando a área do gráfico entre s = 0 e s = 200 :

A 1 = 100 3 2 = 150

A 2 = 100 3 = 300

A 3 = 100 4 = 400

A 4 = 100 2 2 = 100

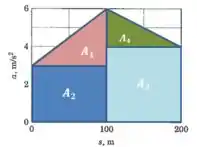
E somando tudo isso temos:

1 2 v 2 = ∫ 0 200 a   d s = 950

v ≅ 43,6   m / s

Passo 3

A agora queremos achar a derivada d v / d s no ponto s = 200   m , vamos voltar à equação de antes:

a = v d v d s

Acabamos de calcular que v = 43,6   m / s e pelo gráfico podemos ver que a = 4   m / s 2 :

4 = 43,6 d v d s

d v d s ≅ 0,0918   s - 1

Pronto!

Resposta

A velocidade é v = 43,6   m / s e o valor da derivada é 0,0918   s - 1 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

3/42) Se a esfera de aço do Prob. 3/41 é liberada a partir do repouso na superfície de um líquido no qual a resistência ao movimento é R = c v 2 , onde c é uma constante e v é a velocidade da esfera p
3/43) Determine a faixa de variação da força aplicada P para a qual o bloco de massa m 2 não escorregará sobre o bloco em formato de cunha de massa m 1 . Despreze o atrito associado com as rodas do bl
3/46) Duas esferas de ferro , cada uma das quais com 100m m de diâmetro , são liberadas a partir do repouso com uma separação de centro de 1m . Suponha um lugar no espaço sem nenhuma força , além da f
3/44) Os cursores A e B estão conectados por uma barra leve rígida de comprimento l = 0,5m e se deslocam com atrito desprezível nos rasgos horizontais mostrados . Para a posição onde x A = 0,4m , a ve
3/39) Calcule a aceleração do bloco A para o instante representado . Despreze as massas das polias .