Uma partícula oscila ao longo de uma linha reta com uma velocidade variando senoidalmente em milímetros por segundo dada por , onde é em segundos. Se o deslocamento da partícula é de quando , determine o seu deslocamento máximo e represente graficamente contra para um ciclo completo.

Nosso primeiro objetivo agora é achar o deslocamento máximo, ou seja, qual o valor máximo que assume?

Lembrando que o cosseno sempre varia entre e , é fácil ver que a função vai ser máxima quando:

E nesse caso:

E agora só falta desenhar o gráfico de em função de :

Como temos uma função trigonométrica, vamos seguir os seguintes passos para esboçar o gráfico.

Primeiro vamos encontrar o valor quando :

E já sabemos que o valor máximo é:

E o valor mínimo ocorre justamente em . Para entender isso, olhe pare esse termo:

O menor valor que ele assume é , e nesse caso teremos:

Para completar o esboço do gráfico, precisamos achar o comprimento de um período completo. O período depende apenas do cosseno:

Quando tempo ele demora para se repetir? Bom, o cosseno se repete depois que o argumento varia de até , ou seja, precisamos achar dois valores de :

Com essas informações já podemos esboçar o gráfico:

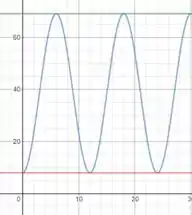
Pronto!