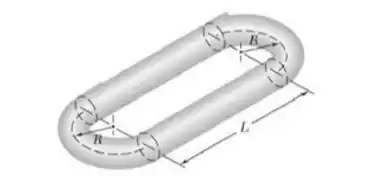
Determine o volume e a área da superfície do elo de corrente mostrado na figura, que é feito de uma barra de de diâmetro, se e .

Fala aí galera, vamos pra mais um problema de estática. O problema quer que a gente determine o volume e a área do elemento da figura. Para isso, vamos utilizar o teorema de Pappus para área e para o volume. Primeiro, vamos calcular volume. Fica assim:

Onde é o volume das barras de comprimento e , é o volume das bordas formadas por semicircunferências. Vamos calculá-los pelo teorema de pappus: