Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 11.Problemas - Ex. 18

Uma mesa de servir uniforme de 5   k g está apoiada em cada lado por um par de membros idênticos, A B e C D , e molas C E . Se a tigela tem massa de 1   k g e está em equilíbrio quando θ = 45 ° , determine a rigidez k de cada mola. As molas não estão deformadas quando θ = 90 ° . Despreze a massa dos membros.

Passo 1

Oi pessoal? Vamos para mais um exercício?

Temos algumas condições de trabalho e queremos o valor da rigidez da mola.

Imagine o seguinte diagrama de corpo livre:

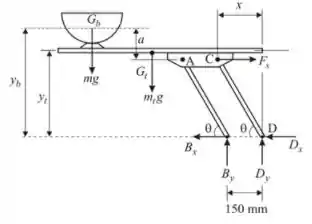
Também temos que esboçar a posição deslocada do sistema sobre o diagrama de corpo livre, quando o sistema sofre um deslocamento virtual:

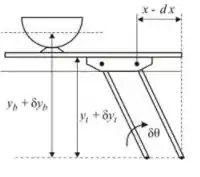
Passo 2

A partir da geometria da figura, vamos equacionar as posições. Temos que:

y b = A B sen ⁡ θ + a

y b = 250 sen ⁡ θ + a

Também temos que:

x = C D cos ⁡ θ

x = 250 cos ⁡ θ

E:

y t = A B sen ⁡ θ

y t = 250 sen ⁡ θ

Para os deslocamentos virtuais, temos que:

δ y b = 250 cos ⁡ θ δ θ

δ y t = 250 cos ⁡ θ δ θ

Passo 3

Quando θ = 90 ° a mola não sofre alongamento. Portanto, podemos dizer que:

s = x - x θ = 90 °

s = 250 cos ⁡ θ - 250 cos ⁡ 90 °

s = 250 cos ⁡ θ

Logo, o seu deslocamento virtual será:

δ s = - 250 sen ⁡ θ δ θ

A força na mola será:

F = k s

F = k ⋅ 250 cos ⁡ θ

Passo 4

Agora é só aplicar o principio do trabalho virtual. Temos que:

δ U = 0

- W b δ y b - W t δ y t - 2 F δ s = 0

Substituindo os dados, temos que:

- M g 250 cos ⁡ θ δ θ - M t g 250 cos ⁡ θ δ θ - 2 ⋅ 250 ⋅ k cos ⁡ θ - 250 sin ⁡ θ δ θ = 0

Sabendo que o trabalho virtual causado por uma força da mola só é positivo se δ s for negativo, temos que:

- M g - M t g - 500 ⋅ k - sin ⁡ θ 250 cos ⁡ θ δ θ = 0

Como a sentença:

250 cos ⁡ θ δ θ ≠ 0

Temos que:

- M g - M t g - 500 ⋅ k - sin ⁡ θ = 0

Substituindo os dados, temos que:

- 1 ( 9,81 ) - ( 5 ) ( 9,81 ) - 500 ⋅ k - sin ⁡ 45 °

k = 0,1664   N / m m

Ou:

k = 166,4   N / m

Resposta

k = 166,4   N / m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

30- Expresse a força compressiva C no cilindro hidráulico da plataforma para carros em termos do ângulo θ . A massa da plataforma é desprezível comparada com a massa m do veículo.
O pequeno cilindro de massa me raio r está confinado a rolar na superfície circular do raio R. Pelos métodos deste artigo, prove que o cilindro é instável no caso (a) e estável no caso (b).
A barra uniforme de massa m e comprimento L é suportada no plano vertical por duas molas idênticas, cada uma de rigidez k e comprimida a uma distância δ na posição vertical θ = 0. Determine a rigidez
No mecanismo mostrado, a haste AB desliza através do colar articulado em O e comprime a mola quando o par M é aplicado para ligar GF para aumentar o ângulo θ. A mola possui uma rigidez k e seria desco