Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.5 - Ex. 76
Calcule o volume V do sólido gerado pela revolução de 180° do triângulo retângulo em torno do eixo z.
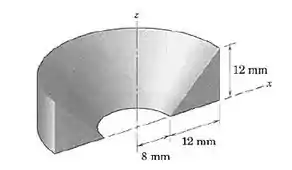
Passo 1
OPA, como você tá? Espero que bem, simbora resolver mais uma questão acerca de Teorema de Pappus, SE VOCÊ ESTÁ AQUI, então creio que saiba centro de massa, por isso, não me aprofundarei acerca desse assunto, se você não sabe centro de massa, então, procura o conteúdo no Responde Aí referente a isso e depois volta, ENFIM, AQUI ESTÁ AS EQUAÇÕES QUE USAREMOS:
(1)
(2)
(3)
A equação 1 é o teorema de Pappus relacionado a volume de um corpo, a equação 2 calcula o centro de massa da secção triangular do corpo e a equação 3 determina a área da secção triangular, DITO ISTO, SIMBORA...
Passo 2
Analisando a figura e o enunciado, obtemos os valores do lado e do ângulo: l = 12mm, = 180° = , com isso, podemos aplicar os dados coletados nas equações e desse modo, conseguir o resultado, então, SIMBORA:
COM ISSO, temos a distância do centro de massa ao eixo y, calculando a área da secção:
YUPIE, com esses valores, agora podemos jogar tudo na equação para descobrir o volume, lembrando que é o ângulo de revolução realizado no eixo y:
YEAAH, menos uma, é isso aí, BORA CONTINUAR NOS ESTUDOS, até a próxima.