Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.5 - Ex. 78

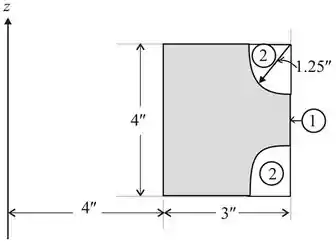
Calcule o volume V do anel que tem a seção transversal mostrada.

Passo 1

Vamos primeiro achar a área com base numa visão melhor da imagem abaixo!

Passo 2

Calculando os volumes

V 1 = 2 π r 1 A 1 = 2 π 4 + 3 2 4 ⋅ 3 = 415   P o l e g a d a s 3

V 2 = - 2 2 π r 2 A 2 = - 4 π 7 - 4 1.25 3 π π 1.25 2 4 = - 99.8     P o l e g a d a s 3

V t o t a l = V 1 + V 2 = 315   P o l e g a d a s 3

Resposta

V t o t a l = 315   P o l e g a d a s 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine por integração direta o centroide da área a seguir. Determine sua resposta em termos de a e b .
Determine por integração direta o centroide da área a seguir. Determine sua resposta em termos de a e h .
Determine as coordenadas do centroide por integração em termos de a e b :
Determine por integração direta o centroide da área mostrada na figura.
Determine por integração direta o centroide da área mostrada na figura.