Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 8.Problemas - Ex. 119

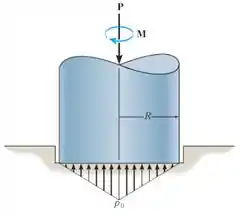
Devido ao desgaste nas bordas, o mancal axial está sujeito a uma distribuição de pressã cônica em sua superfície de contato. Determine o torque M necessário para superar o atrito e girar o eixo, que suporta uma força axial P . O coeficiente de atrito estático é μ s . Para a solução, é preciso determinar a pressão de pico p 0 em termos de P e o raio do rolamento R .

Passo 1

Vamos desenhar o diagrama de corpo livre dessa situação para entendermos a situação da nossa questão!

Passo 2

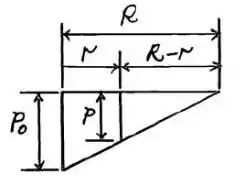
Aqui vamos precisar um pouco da nossa querida geometria plana, pessoal! Vamos usar a semalhança de triângulos para escrever p em função de p o , R e r .

p o R = p R - r

p = p o R ( R - r )

O elemento diferencial de área pode ser escrito como d A = 2 π r d r , levando a seguinte expressão para o diferencial da normal d N = p d A = p ( 2 π r d r ) e d F = μ s d N .

Passo 3

Para um sistema em equilíbrio, a soma das forças nos eixos de referência ( x , y , z ) e o momento em relação a um ponto devem ser iguais a zero. Assim, vamos analisar o somatório de forças na vertical. Assumindo como positivo a direção para cima, temos:

N - P = 0

∫ p d A - P = 0

∫ p o R R - r 2 π r d r - P = 0

2 π p o R ∫ 0 R r R - r d r - P = 0

p o = 3 P π R ²

Passo 4

Vamos agora fazer a análise para o momento. Assumindo o sentido anti-horário como positivo, temos:

∑ M z = 0

∫ ( μ s p d A ) r - M = 0

∫ 0 R μ s p o R R - r 2 π r d r r - M = 0

2 π μ s p o R ∫ 0 R r 2 R - r d r - M = 0

M = π μ s R 3 p o 6

Subsituindo a equação encontrada no passo anterior nessa, temos:

M = π μ s R 3 6 3 P π R 2

M = μ s P R 2

Resposta

o torque M necessário para superar o atrito e girar o eixo:

M = μ s P R 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

141- Um cabo pesado, com massa de 12k g por metro de comprimento, passa sobre os dois tubos presos distantes 300m entre si, e em um mesmo nível. Uma extremidade sustenta um cilindro de 1600k g . Exper
O caixote de 10 Mg é abaixado para uma câmara de armazenamento subterrânea em um elevador de dois parafusos projetado como mostrado. Cada parafuso tem uma massa de 0,9 Mg, um diâmetro médio de 120 mm
A figura mostra uma transmissão de vários discos projetada para uso marítimo. Os discos de potência A são encaixados em uma canaleta no eixo, mas têm que girar com ele. Os discos C atuam sobre a estru
Um mancal radial para um eixo sob uma carga axial L é projetado como um copo esférico parcial de raio r . Se a pressão entre as superfícies do mancal em qualquer ponto varia de acordo com p = p 0 cos
Determine a expressão para o torque M necessário para girar o eixo cuja pressão axial L é sustentada por um mancal cômico. O coeficiente de atrito é μ , e a pressão no mancal é constante.