Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 11.Problemas - Ex. 25
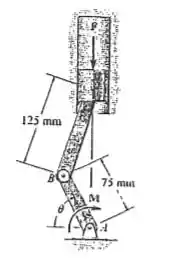
O virabrequim está sujeito a um torque . Determine a força compressiva vertical aplicada ao pistão para o equilíbrio quando
Passo 1
Fala ai galerinha bonita, tudo beleza?
Nesse exercício aqui a gente quer encontrar qual a força necessária para manter o virabrequim em equilíbrio dado um ângulo e um momento binário .
Iradoso, então podemos usar os conceitos de trabalho virtual pra ajudar a gente nessa tarefa. Vamos ter que:
Pra isso vamos precisar encontrar a distância e distância virtual que atua:
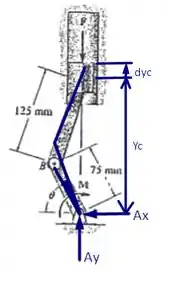
Bora lá encontrar esse danadinho!
Passo 2
Como conhecemos dois lados e um ângulo, podemos usar a lei dos cossenos, de modo que:
E como , vamos ter que:
Iradoso, agora se a gente derivar isso implicitamente, vamos obter:
Isolando :
Passo 3
Show de bola, então se a gente substituir na nossa equação do trabalho virtual, vamos obter que:
De modo que:
Então em , se a gente aplicar na equação que conseguimos a partir da lei dos cossenos:
Vamos obter uma equação do segundo grau, cujo a única raiz positiva vai ser:
E como temos , passando para pra não ter unidade diferente nos cálculos, teremos , de modo que será: