Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 66

O diagrama cinético representando o movimento rotacional geral de um corpo rígido em torno de um eixo fixo passando por O é mostrado na figura. Mostre que I G α pode ser eliminado deslocando os vetores m a G t e m a G n para o ponto P, localizado a uma distância r G P = k G 2 / r O G do centro de massa G do corpo. Aqui, k G representa o raio de giração do corpo em relação a um eixo passando por G. O ponto P é chamado de centro de percussão do corpo.

Passo 1

Sabemos que o momento de inércia I G é dado por:

I G = m k G 2

Sendo assim, com o auxílio da figura a seguir:

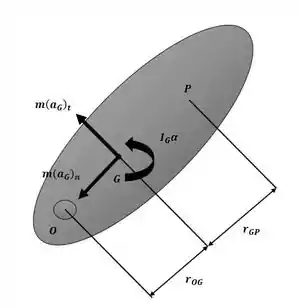
Podemos escrever:

m a G t r O G + I G α = m a G t r O G + ( m k G 2 ) α

Passo 2

Como foi fornecido no enunciado, sabemos que:

r G P = k G 2 r O G → k G 2 = r O G ( r G P )

Além disso, sabemos também que a aceleração angular se relaciona com a aceleração tangencial pela seguinte fórmula:

a G t = α r O G → α = a G t r O G

Passo 3

Dessa forma, substituindo os valores do passo 2 na última equação do passo 1, temos:

m a G t r O G + I G α = m a G t r O G + ( m k G 2 ) α

m a G t r O G + I G α = m a G t r O G + [ m r O G r G P ] a G t r O G

m a G t r O G + I G α = m a G t ( r O G + r G P )

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O guindaste possui uma lança de comprimento OP = 24 m e está girando em torno do eixo vertical na taxa constante de 2 rpm no sentido indicado. Simultaneamente, a lança está sendo abaixada na taxa cons
O disco circular de 120 mm de raio gira em torno do eixo z na taxa constante de w = 20 rad/s, e o conjunto inteiro gira em torno do eixo fixo x na taxa constante wx = 10 rad/s. Calcule os módulos da v
O robô apresentado possui 5 graus de liberdade de rotação. Os eixos x-y-z estão presos no anel da base, que gira em torno do eixo Z com velocidade angular w1. O braço de O1O2 gira em torno do eixo x c
A roda rola sem deslizar em um eixo circular de raio R e faz uma volta completa em torno do eixo vertical y om velocidade constante em um tempo τ . Determine as expressões para a velocidade v e a acel
A extremidade do elemento de ligação A está soldada ao garfo que é articulado em relação ao eixo z ao cursor C. O cursor pode girar em torno do eixo x da barra fixa. O elemento de ligação A e seu garf