C
B
Passo 1
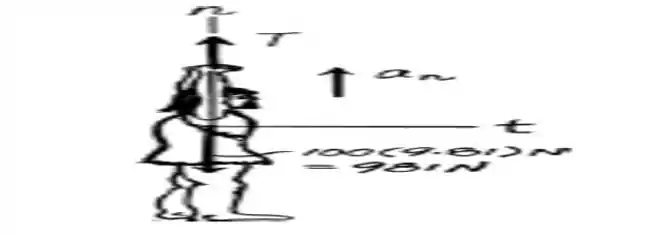
Fig. B
Fig. A
Passo 2
Analisando os estágios do sistema:
Estágio C: Origem do sistema.
- Pela referência definida, tem-se que a consequência imediata será = 0.
- Tarzan parte do repouso, isto é, =0.
Estágio B: Posição de chegada.
- A partir da Fig. A e o ponto de referência, obtém-se que .
- De B até o centro de massa do Tarzan, tem-se uma distância de 10 m. Note que a trajetória executada será de natureza curvilínea, tornando adequada uma análise com o sistema de coordenadas normal-tangencial. Assim, a distância de 10 m é caracterizada como o raio de curvatura.
Passo 3
Identificadas as energias atuantes no sistema, admitindo que sejam conservativas, a lei de conservação da energia mecânica será:
Substituindo as expressões no balanço energético e sabendo que as constantes elásticas são iguais, tem-se que:
Passo 4
Devido às conclusões acerca dos estágios B e C definidas nos passos anteriores, tem-se que:
Passo 5
Determinada a velocidade na chegada ao ponto B, é necessária ainda a força necessária que o Tarzan deve executar imediatamente antes e depois de realizar o contato com o galho B. Devido à trajetória curvilínea, o sistema de coordenadas mais adequado é o n-t (normal-tangencial), definido na Fig. B.
Análises dinâmicas:
- Imediatamente antes de entrar em contato com B, ρ = 10 m.
- Imediatamente depois de entrar em contato com B, ρ = 10 - 7 = 3 m.
Note que, pelo sistema de coordenadas, não há realização de forças na direção tangencial, somente na direção normal especificamente a tração realizada na corda, dessa forma:
As forças através do diagrama de corpo livre da Fig. B expressam as forças atuantes na corda, isto é, o peso do Tarzan e a tração na corda, resultando:
Resposta
A velocidade de chegada ao ponto B será de 7,581 m/s e as forças necessárias pelo Tarzan imediatamente antes e depois da chegada ao galho B são, respectivamente, 1,556 kN e 2,897 kN.